
【题目】如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.
(1)求证:AE=CF;
(2)若∠ABE=55°,求∠EGC的大小.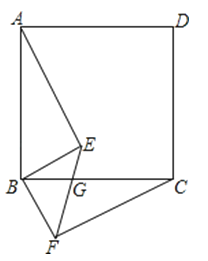
【答案】(1)证明:∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC,
∵BE⊥BF,
∴∠FBE=90°,
∵∠ABE+∠EBC=90°,∠CBF+∠EBC=90°,
∴∠ABE=∠CBF,
在△AEB和△CFB中,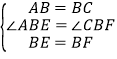
∴△AEB≌△CFB(SAS),
∴AE=CF.
(2)解:∵BE⊥BF,
∴∠FBE=90°,
又∵BE=BF,
∴∠BEF=∠EFB=45°,
∵四边形ABCD是正方形,
∴∠ABC=90°,
又∵∠ABE=55°,
∴∠EBG=90°﹣55°=35°,
∴∠EGC=∠EBG+∠BEF=45°+35°=80°.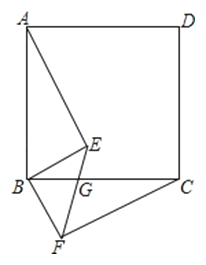
【解析】(1)利用△AEB≌△CFB来求证AE=CF.
(2)利用角的关系求出∠BEF和∠EBG,∠EGC=∠EBG+∠BEF求得结果.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠B=60',∠D=50°,将△CMN沿MN翻折得△EMN,若EM∥AB,EN∥AD,则∠C的度数为

A. 110° B. 115° C. 120° D. 125°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴,y轴分别交于B,C两点,抛物线
与x轴,y轴分别交于B,C两点,抛物线![]() 过点B,C.
过点B,C.
(1)求b、c的值;
(2)若点D是抛物线在x轴下方图象上的动点,过点D作x轴的垂线,与直线BC相交于点E.当线段DE的长度最大时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD中,点O是对角线DB的中点,点P是DB所在直线上的一个动点,PE⊥BC于E,PF⊥DC于F.
(1)当点P与点O重合时(如图①),猜测AP与EF的数量及位置关系,并证明你的结论;
(2)当点P在线段DB上(不与点D、O、B重合)时(如图②),探究(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由;
(3)当点P在DB的长延长线上时,请将图③补充完整,并判断(1)中的结论是否成立?若成立,直接写出结论;若不成立,请写出相应的结论.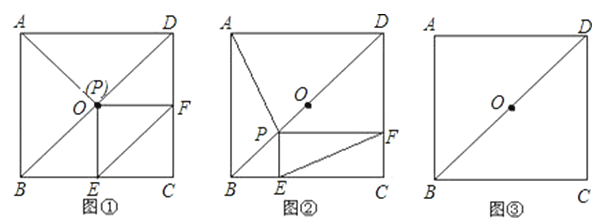
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查适合采用抽样调查的是( )
A. 某公司招聘人员,对应聘人员进行面试
B. 调查一批节能灯泡的使用寿命
C. 为保证火箭的成功发射,对其零部件进行检查
D. 对乘坐某次航班的乘客进行安全检查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象经过点A(4,0),直线y=﹣3x+3与x轴交于点B,与y轴交于点D,且两直线交于点C(2,m).
(1)求m的值及一次函数的解析式;
(2)求△ACD的面积.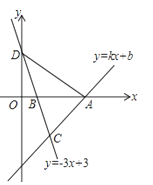
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com