
【题目】如图,O为坐标原点,四边彤OACB是菱形,OB在x轴的正半轴上,sin∠AOB=![]() ,反比例函数
,反比例函数![]() 在第一象限内的图象经过点A,与BC交于点F,删△AOF的面积等于( )
在第一象限内的图象经过点A,与BC交于点F,删△AOF的面积等于( )

A. 10 B. 9 C. 8 D. 6
【答案】A
【解析】 过点A作AM⊥x轴于点M,过点F作FN⊥x轴于点N,设OA=a,BF=b,通过解直角三角形分别找出点A、F的坐标,结合反比例函数图象上点的坐标特征即可求出a、b的值,通过分割图形求面积,最终找出△AOF的面积等于梯形AMNF的面积,利用梯形的面积公式即可得出结论.
解:过点A作AM⊥x轴于点M,过点F作FN⊥x轴于点N,如图所示.
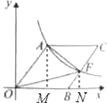
设OA=a,BF=b,
在Rt△OAM中,∠AMO=90°,OA=a,sin∠AOB=![]() ,
,
∴AM=OAsin∠AOB=![]() a,OM=
a,OM=![]() =
=![]() a,
a,
∴点A的坐标为(![]() a,
a, ![]() a).
a).
∵点A在反比例函数y=![]() 的图象上,
的图象上,
∴![]() a×
a×![]() a=
a=![]() a2=12,
a2=12,
解得:a=5,或a=﹣5(舍去).
∴AM=8,OM=6.
∵四边形OACB是菱形,
∴OA=OB=10,BC∥OA,
∴∠FBN=∠AOB.
在Rt△BNF中,BF=b,sin∠FBN=![]() ,∠BNF=90°,
,∠BNF=90°,
∴FN=BFsin∠FBN=![]() b,BN=
b,BN=![]() =
=![]() b,
b,
∴点F的坐标为(10+![]() b,
b, ![]() b).
b).
∵点F在反比例函数y=![]() 的图象上,
的图象上,
∴(10+![]() b)×
b)×![]() b=12,
b=12,
S△AOF=S△AOM+S梯形AMNF﹣S△OFN=S梯形AMNF=10
故选A.
“点睛”本题主要考查了菱形的性质、解直角三角形以及反比例函数图象上点的坐标特征,解题的关键是找出S△AOF=![]() S菱形OBCA.
S菱形OBCA.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:初中数学 来源: 题型:
【题目】在直角△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于D,CE是△ABC的角平分线. 
(1)求∠DCE的度数.
(2)若∠CEF=135°,求证:EF∥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O(0,0),B(0,1)是正方形OBB1C的两个顶点,以它的对角线OB1为一边作正方形OB1B2C1 , 以正方形OB1B2C1的对角线OB2为一边作正方形OB2B3C2 , 再以正方形OB2B3C2的对角线OB3为一边作正方形OB3B4C3 , …,依次进行下去,则点B6的坐标是 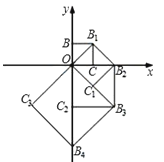
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 必然事件发生的概率是1
B. 通过大量重复试验,可以用频率估计概率
C. 概率很小的事件不可能发生
D. 投一枚图钉,“钉尖朝上”的概率不能用列举法求得
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠B=60',∠D=50°,将△CMN沿MN翻折得△EMN,若EM∥AB,EN∥AD,则∠C的度数为

A. 110° B. 115° C. 120° D. 125°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD中,点O是对角线DB的中点,点P是DB所在直线上的一个动点,PE⊥BC于E,PF⊥DC于F.
(1)当点P与点O重合时(如图①),猜测AP与EF的数量及位置关系,并证明你的结论;
(2)当点P在线段DB上(不与点D、O、B重合)时(如图②),探究(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由;
(3)当点P在DB的长延长线上时,请将图③补充完整,并判断(1)中的结论是否成立?若成立,直接写出结论;若不成立,请写出相应的结论.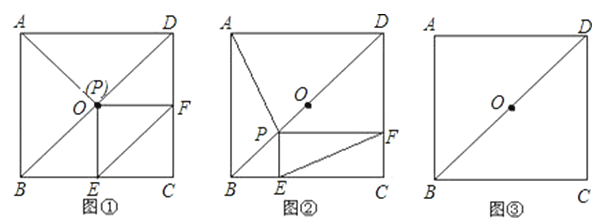
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解一元二次方程x2﹣4x=5时,此方程可变形为( )
A.(x+2)2=1
B.(x﹣2)2=1
C.(x+2)2=9
D.(x﹣2)2=9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com