
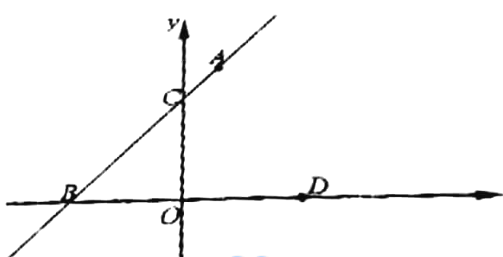
【题目】如图,已知一次函数y=kx+3的图形经过点A (1, m),与x轴、y轴分别相交于B、C两点,且∠ABO=45°,设点D的坐标为(3,0)
(1) 求m的值;
(2) 联结CD、AD,求△ACD的面积;
(3) 设点E为x轴上一动点,当∠ADC=∠ECD时,求点E的坐标.
【答案】(1)m=4;(2)![]() ;(3)点E的坐标为(
;(3)点E的坐标为(![]() ,0)或(6,0).
,0)或(6,0).
【解析】
(1)求出点B坐标,利用待定系数法求出直线BC的解析式即可解决问题;
(2)根据![]() 进行计算即可;
进行计算即可;
(3)分点E在点D左侧和点E在点D右侧两种情况,分别求出直线CE1和直线CE2的解析式即可得到对应的点E的坐标.
解:(1)∵一次函数y=kx+3的图象与x轴、y轴分别相交于B、C两点,∠ABO=45°,
∴OB=OC=3,
∴B(-3,0),
将B(-3,0)代入y=kx+3得:0=-3k+3,
解得:k=1,
∴直线BC的解析式为:y=x+3,
当x=1时,y=x+3=4,
∴m=4;
(2)∵B(-3,0),C(0,3),D(3,0),A(1,4),
∴BD=6,
∴![]() ;
;
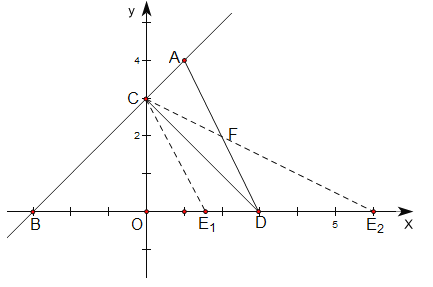
(3)如图所示,当点E在点D左侧时,
∵∠ADC=∠E1CD,
∴AD∥CE1,
设直线AD的解析式为:y=k1x+b(k≠0),
代入A(1,4),D(3,0)得: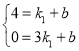 ,解得:
,解得:![]() ,
,
∴直线AD的解析式为:![]() ,
,
故设直线CE1的解析式为:![]() ,
,
代入C(0,3)得:![]() ,
,
∴直线CE1的解析式为:![]() ,
,
当y=0时,解得:![]() ,
,
∴E1(![]() ,0);
,0);
当点E在点D右侧时,AD与CE2交于点F,
∵∠ADC=∠E2CD,
∴FC=FD,
∵OB=OD=3,∠ABO=45°,
∴∠CDB=45°,
∴∠ACD=45°+45°=90°,即∠ACF+∠FCD=90°,
∵∠CAF+∠FDC=90°,
∴∠ACF=∠CAF,
∴FC=FA,
∴F为线段AD的中点,
∴点F的坐标为![]() ,
,
设直线CE2的解析式为:![]() ,
,
代入F![]() 得:
得:![]() ,解得:
,解得:![]() ,
,
∴直线CE2的解析式为:![]() ,
,
当y=0时,解得:![]() ,
,
∴E2(6,0),
综上所述,点E的坐标为(![]() ,0)或(6,0).
,0)或(6,0).


科目:初中数学 来源: 题型:
【题目】为了改善小区环境,某小区决定要在一块一边靠墙(墙长 25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为 40m 的栅栏围住(如图).设绿化带的BC 边长为x m,绿化带的面积为y m2 . 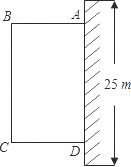
(1)求y 与x 之间的函数关系式,并写出自变量x 的取值范围.
(2)当x 为何值时,满足条件的绿化带的面积最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线BC//ED.
(1)如图1,若点A在直线DE上,且∠B=44°,∠EAC=57°,求∠BAC的度数;
(2)如图2,若点A是直线DE的上方一点,点G在BC的延长线上求证:∠ACG=∠BAC+∠ABC;
(3)如图3,FH平分∠AFE,CH平分∠ACG,且∠FHC比∠A的2倍少60°,直接写出∠A的度数.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).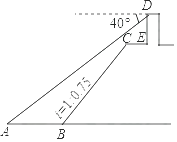
A.5.1米
B.6.3米
C.7.1米
D.9.2米
查看答案和解析>>
科目:初中数学 来源: 题型:
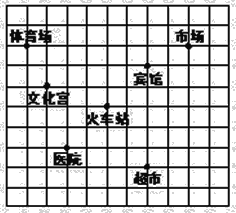
【题目】如图,这是某市部分简图,为了确定各建筑物的位置:
(1)请你以火车站为原点建立平面直角坐标系﹒
(2)写出超市的坐标(小正方形网格的单位长度为1)﹒
(3)请将体育场、宾馆和火车站看作三点,用线段连接起来,得到三角形ABC,然后将此三角形向下平移4个单位,再画出平移后的三角形A′B′C′,并计算三角形A′B′C′的面积﹒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在黄冈长江大桥的东端一处空地上,有一块矩形的标语牌ABCD(如图所示),已知标语牌的高AB=5m,在地面的点E处,测得标语牌点A的仰角为30°,在地面的点F处,测得标语牌点A的仰角为75°,且点E,F,B,C在同一直线上,求点E与点F之间的距离.(计算结果精确到0.1米,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)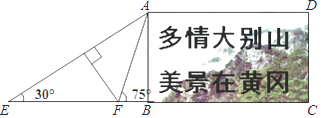
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人骑自行车前往A地,他们距A地的路程s(km)与行驶时间t(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:

(1)甲、乙两人的速度各是多少?
(2)求出甲距![]() 地的路程
地的路程![]() 与行驶时间
与行驶时间![]() 之间的函数关系式.
之间的函数关系式.
(3)在什么时间段内乙比甲离![]() 地更近?
地更近?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形 ABCD 中,E 为 BC 的中点,F 是 CD 上一点,且 CF ![]() CD ,
CD ,

求证:(1)∠AEF=90°;
(2) ∠BAE=∠EAF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别是4、5、6,则四边形DHOG的面积是( )
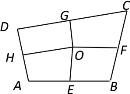
A. 5B. 4C. 8D. 6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com