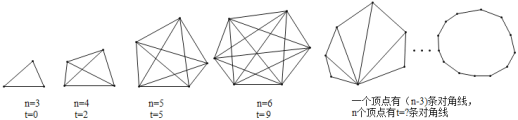
【题目】如图，先研究下面三角形、四边形、五边形、六边形…多边形的边数n及其对角线条数t的关系，再完成下面问题：
（1）若一个多边形是七边形，它的对角线条数为 ，n边形的对角线条数为t＝ （用n表示）．
（2）求正好65条对角线的多边形是几边形．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】.已知：在矩形
中，
是对角线，
于点
，
于点
；
（1）如图1，求证：
；
（2）如图2，当
时，连接
.
，在不添加任何辅助线的情况下，请直接写出图2中四个三角形，使写出的每个三角形的面积都等于矩形面积的
.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】教育部基础教育司负责人解读“2020新中考”时强调要注重学生分析与解决问题的能力，要增强学生的创新精神和综合素质.王老师想尝试改变教学方法，将以往教会学生做题改为引导学生会学习.于是她在菱形的学习中，引导同学们解决菱形中的一个问题时，采用了以下过程（请解决王老师提出的问题）：
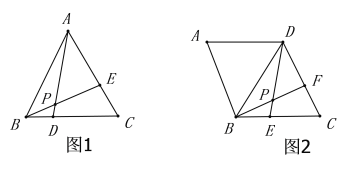
先出示问题（1）:如图1，在等边三角形
中，
为
上一点，
为
上一点，如果
，连接
、
，、相交于点
，求
的度数.
通过学习，王老师请同学们说说自己的收获.小明说发现一个结论：在这个等边三角形中，只要满足，则的度数就是一个定值，不会发生改变.紧接着王老师出示了问题（2）:如图2，在菱形
中，
，为上一点，
为
上一点，
，连接
、
，、相交于点，如果
，
，求出菱形的边长.
问题（3）：通过以上的学习请写出你得到的启示（一条即可）.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在
中，AB=AC，以AB为直径作⊙O，分别交BC于点D，交CA的延长线于点E，过点D作
于点H，连接DE交线段OA于点F．
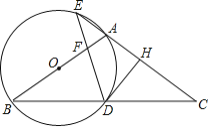
（1）试猜想直线DH与⊙O的位置关系，并说明理由；
（2）若AE=AH，EF=4，求DF的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
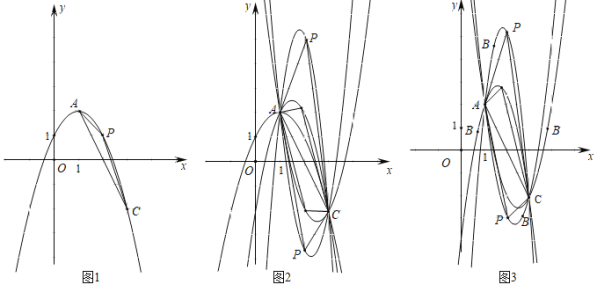
【题目】定义：连接抛物线上两点的线段叫抛物线的弦，在这两点之间抛物线上的任意一点P与此两点构成的三角形称作抛物线的弦三角，点P称作弦锥，设点P的横坐标为x．
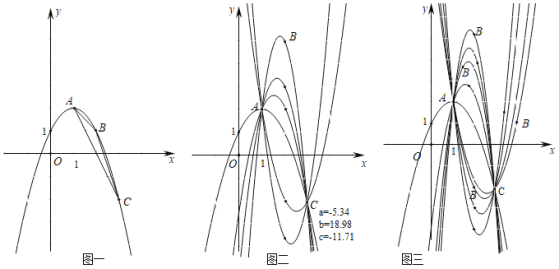
已知抛物线经过A（1，2）、B（m，n）、C（3，﹣2）三点，P是抛物线上AC之间的一点，以AC为弦的弦三角为△PAC.
（1）图一，当m＝2，n＝1时，求该抛物线的解析式，若x＝k1时△PAC的面积最大，求k1的值．
（2）图二，当m＝2，n≠1时，用n表示该抛物线的解析式，若x＝k2时△PAC的面积最大，求k2的值．k1与k2有何数量关系？
（3）图三，当m≠2，n≠1时，用m，n表示该抛物线的解析式，若x＝k3时△PAC的面积最大，求k3的值．观察图1，2，3，过定点A、C，根据B在各种不同位置所得计算结果，你发现通过两个定点的抛物线系中，以此两点为弦的弦三角的面积取得最大值时，弦锥的横坐标有何规律？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，OA⊥OB，AB⊥x轴于点C，点A（
，1）在反比例函数
的图象上．
（1）求反比例函数
的表达式；
（2）在x轴的负半轴上存在一点P，使得S△AOP=
S△AOB，求点P的坐标；
（3）若将△BOA绕点B按逆时针方向旋转60°得到△BDE．直接写出点E的坐标，并判断点E是否在该反比例函数的图象上，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在一个可以自由转动的转盘中，指针位置固定，三个扇形的面积都相等，且分别标有数字1，2，3．
（1）小明转动转盘一次，当转盘停止转动时，指针所指扇形中的数字是奇数的概率为 ；
（2）小明先转动转盘一次，当转盘停止转动时，记录下指针所指扇形中的数字；接着再转动转盘一次，当转盘停止转动时，再次记录下指针所指扇形中的数字，求这两个数字之和是3的倍数的概率（用画树状图或列表等方法求解）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】岳阳市整治农村“空心房”新模式，获评全国改革开放40年地方改革创新40案例．据了解，我市某地区对辖区内“空心房”进行整治，腾退土地1200公顷用于复耕和改造，其中复耕土地面积比改造土地面积多600公顷．
（1）求复耕土地和改造土地面积各为多少公顷；
（2）该地区对需改造的土地进行合理规划，因地制宜建设若干花卉园和休闲小广场，要求休闲小广场总面积不超过花卉园总面积的
，求休闲小广场的总面积最多为多少公顷．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
