
如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是x=1,下列结论正确的是( )
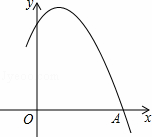
A. b2>4ac B.ac>0 C.a﹣b+c>0 D. 4a+2b+c<0
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
如图,∠A0B的两边0A,0B均为平面反光镜,∠A0B=40°.在射线0B上有一点P,从P点射出一束光线经0A上的Q点反射后,反射光线QR恰好与0B平行,则∠QPB的度数是( )
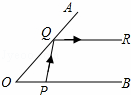
A. 60° B.80° C.100° D. 120°
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,﹣1)和C(4,5)三点.
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.
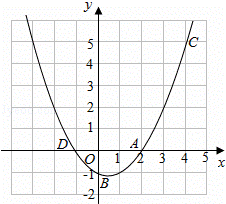
查看答案和解析>>
科目:初中数学 来源: 题型:
某厂今年一月份新产品的研发资金为a元,以后每月新产品的研发资金与上月相比增长率都是x,则该厂今年三月份新产品的研发资金y(元)关于x的函数关系式为y= .
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
(1)请直接写出D点的坐标.
(2)求二次函数的解析式.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.
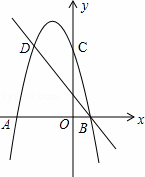
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,已知点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一根长为2014个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是 .
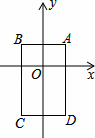
查看答案和解析>>
科目:初中数学 来源: 题型:
园林队在某公园进行绿化,中间休息了一段时间.已知绿化面积S(单位:平方米)与工作时间t(单位:小时)的函数关系的图象如图,则休息后园林队每小时绿化面积为( )
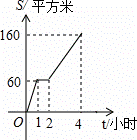
A. 40平方米 B.50平方米 C.80平方米 D. 100平方米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com