
分析 现根据分式的混合运算顺序和法则化简原式,再代入求解即可得.
解答 解:原式=[$\frac{{n}^{2}}{n-m}$-(m+n)]•$\frac{1}{{m}^{2}}$
=$\frac{{n}^{2}-{n}^{2}+{m}^{2}}{n-m}$•$\frac{1}{{m}^{2}}$
=$\frac{{m}^{2}}{n-m}$•$\frac{1}{{m}^{2}}$
=$\frac{1}{n-m}$,
∵m-n=$\sqrt{2}$,
∴n-m=-$\sqrt{2}$,
则原式=$\frac{1}{-\sqrt{2}}$=-$\frac{\sqrt{2}}{2}$.
点评 本题主要考查分式的化简求值,熟练掌握分式的混合运算顺序和运算法则是解题的关键.


科目:初中数学 来源: 题型:解答题
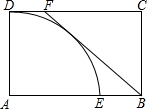 如图,矩形ABCD,AB=3,AD=2,以点A为圆心,AD长为半径的DE交AB于E,DF=0.8,判断直线BF与DE所在的圆的位置关系.
如图,矩形ABCD,AB=3,AD=2,以点A为圆心,AD长为半径的DE交AB于E,DF=0.8,判断直线BF与DE所在的圆的位置关系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
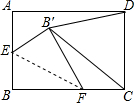 如图,在矩形ABCD中,AB=6,BC=8,点E为AB的中点,点F为BC边上任意一点,将△BEF沿EF翻折,点B的对应点为B′,则当△B′CD面积最小时折痕EF的长为3$\sqrt{2}$.
如图,在矩形ABCD中,AB=6,BC=8,点E为AB的中点,点F为BC边上任意一点,将△BEF沿EF翻折,点B的对应点为B′,则当△B′CD面积最小时折痕EF的长为3$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:
如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:| A. | ①②③④ | B. | ②③ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
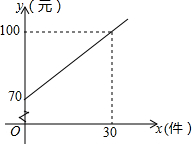 某快递公司的每位“快递小哥”日收入与每日的派送量成一次函数关系,如图所示.
某快递公司的每位“快递小哥”日收入与每日的派送量成一次函数关系,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
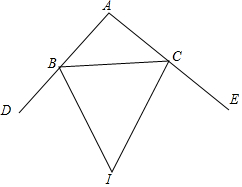 如图,BI,CI分别平分△ABC的外角∠DBC和∠ECB,
如图,BI,CI分别平分△ABC的外角∠DBC和∠ECB,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com