
分析 (1)把抛物线的一般式写成顶点坐标式,进而得到答案;
(2)令y=0,求出x的值,令x=0,求出y的值,即可求出△ABC的面积.
解答 解:(1)抛物线y=$\frac{1}{2}$x2-4x+6=$\frac{1}{2}$(x2-8x+16)-2=$\frac{1}{2}$(x-4)2-2,
即抛物线的开口向上,对称轴为直线x=4,顶点坐标为(4,-2);
(2)令y=$\frac{1}{2}$x2-4x+6=0,
解得x1=2,x2=6,
则AB=4,
令x=0,y=6,
则OC=6,
即△ABC的面积=$\frac{1}{2}$×4×6=12.
点评 本题考查了抛物线与x轴的交点.解题时需要熟悉二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的图象与x轴的交点与一元二次方程ax2+bx+c=0根之间的关系.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,数轴上A点表示的数是a,B点表示的数是b,点A在点B的右边
如图,数轴上A点表示的数是a,B点表示的数是b,点A在点B的右边查看答案和解析>>
科目:初中数学 来源:2017届江苏省扬州市九年级下学期第一次月考数学试卷(解析版) 题型:填空题
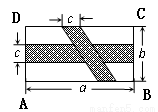
如图,在矩形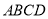 中,横向阴影部分是矩形,另一阴影部分是平行四边形.依照图中标注的数据,计算图中空白部分的面积,已知a=2b=6c,其面积是_________________________.(用含c的代数式表示)
中,横向阴影部分是矩形,另一阴影部分是平行四边形.依照图中标注的数据,计算图中空白部分的面积,已知a=2b=6c,其面积是_________________________.(用含c的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com