
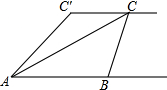
 如图,小敏、小亮从A,B两地观测空中C处一个气球,分别测得仰角为30°和60°,A,B两地相距100 米.当气球沿与BA平行地飘移10秒后到达C′处时,在A处测得气球的仰角为45°.
如图,小敏、小亮从A,B两地观测空中C处一个气球,分别测得仰角为30°和60°,A,B两地相距100 米.当气球沿与BA平行地飘移10秒后到达C′处时,在A处测得气球的仰角为45°.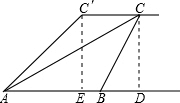
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
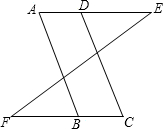 如图,在:①AB∥CD;②AD∥BC;③∠A=∠C中,请你选取其中的两个作为条件,另一个作为结论,写出一个正确命题,并证明其正确性.
如图,在:①AB∥CD;②AD∥BC;③∠A=∠C中,请你选取其中的两个作为条件,另一个作为结论,写出一个正确命题,并证明其正确性.查看答案和解析>>
科目:初中数学 来源: 题型:
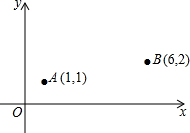 已知A(1,1),B(6,2),C、D分别为x轴、y轴上的动点,在运动的过程中,如果C、D满足|AC-BC|最大,而使|AD+BD|最小,则CD的长为
已知A(1,1),B(6,2),C、D分别为x轴、y轴上的动点,在运动的过程中,如果C、D满足|AC-BC|最大,而使|AD+BD|最小,则CD的长为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com