
【题目】(1)如图1,![]() 中,
中,![]() ,直线
,直线![]() 过点
过点![]() ,点
,点![]() 在直线
在直线![]() 同侧,
同侧,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() 吗?请说明理由;
吗?请说明理由;


(2)如图2,![]() ,且
,且![]() ,
,![]() ,且
,且![]() ,利用(1)中的结论,请按照图中所标注的数据计算图中实线所围成的图形的面积
,利用(1)中的结论,请按照图中所标注的数据计算图中实线所围成的图形的面积![]() = ;
= ;
(3)如图3,等边![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,动点
,动点![]() 从点
从点![]() 沿射线
沿射线![]() 以
以![]() 速度运动,连结
速度运动,连结![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() .请分别求出下列情况点
.请分别求出下列情况点![]() 的运动时间.
的运动时间.
①![]() (直接写出答案);
(直接写出答案);
②点![]() 恰好落在射线
恰好落在射线![]() 上(画出图形,并写出解题过程).
上(画出图形,并写出解题过程).
科目:初中数学 来源: 题型:
【题目】“中国梦”关乎每个人的幸福生活,为进一步感知我们身边的幸福,展现成都人追梦的风采,我市某校开展了以“梦想中国,逐梦成都”为主题的摄影大赛,要求参赛学生每人交一件作品.现将参赛的50件作品的成绩(单位:分)进行统计如下:
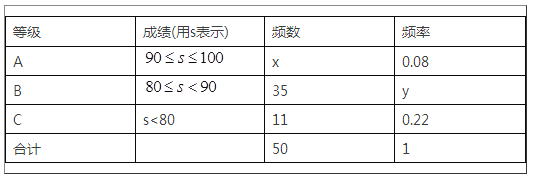
请根据上表提供的信息,解答下列问题:
(1)表中x的值为________,y的值为________;
(2)将本次参赛作品获得A等级的学生依次用A1,A2,A3,…表示,现该校决定从本次参赛作品获得A等级的学生中,随机抽取两名学生谈谈他们的参赛体会,请用树状图或列表法求恰好抽到学生A1和A2的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若△ABC内一点P满足∠PAC=∠PCB=∠PBA,则称点P为△ABC的布罗卡尔点,三角形的布罗卡尔点是法国数学家和数学教育家克雷尔首次发现,后来被数学爱好者法国军官布罗卡尔重新发现,并用他的名字命名,布罗卡尔点的再次发现,引发了研究“三角形几何”的热潮.已知△ABC中,CA=CB,∠ACB=120°,P为△ABC的布罗卡尔点,若PA=![]() ,则PB+PC=_____.
,则PB+PC=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知购买甲型机器人1台,乙型机器人2台,共需14万元;购买甲型机器人2台,乙型机器人3台,共需24万元.
(1)求甲、乙两种型号的机器人每台的价格各是多少万元;
(2)已知甲型和乙型机器人每台每小时分拣快递分别是1200件和1000件,该公司计划购买这两种型号的机器人共8台,总费用不超过41万元,并且使这8台机器人每小时分拣快递件数总和不少于8300件,则该公司有哪几种购买方案?哪个方案费用最低,最低费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC、∠ACB的角平分线交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N.若BM=3cm,CN=2cm,则MN=_____cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE.
(1)求证:BE是⊙O的切线;
(2)当BE=3时,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题引入:
(1)如图1,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC= (用α表示);
如图2,∠CBO=![]() ∠ABC,∠BCO=
∠ABC,∠BCO=![]() ∠ACB,∠A=α,则∠BOC= (用α表示);
∠ACB,∠A=α,则∠BOC= (用α表示);
拓展研究:
(2)如图3,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,猜想∠BOC= (用α表示),并说明理由;
∠ECB,∠A=α,猜想∠BOC= (用α表示),并说明理由;
(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,请猜想∠BOC= .
∠ECB,∠A=α,请猜想∠BOC= .

查看答案和解析>>
科目:初中数学 来源: 题型:
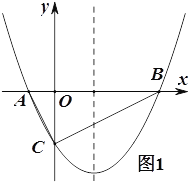
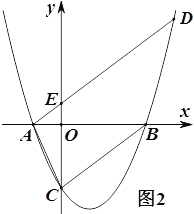
【题目】如图,已知抛物线![]() (
(![]() >0)与
>0)与![]() 轴交于A,B两点(A点在B点的左边),与
轴交于A,B两点(A点在B点的左边),与![]() 轴交于点C。
轴交于点C。
(1)如图1,若△ABC为直角三角形,求![]() 的值;
的值;
(2)如图1,在(1)的条件下,点P在抛物线上,点Q在抛物线的对称轴上,若以BC为边,以点B,C,P,Q为顶点的四边形是平行四边形,求P点的坐标;
(3)如图2,过点A作直线BC的平行线交抛物线于另一点D,交![]() 轴交于点E,若AE:ED=1:4,求
轴交于点E,若AE:ED=1:4,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1所示,写出A、B的坐标:A_________、B________;
(2)如图1所示,将点A向右平移1个单位到点D,点C、B关于y轴对称,求出四边形ABCD的面积;
(3)将图1中的网格去掉得到图2所示,直线AB的交y轴于点C,直线CD⊥AB于点C,△ACD为等腰直角三角形,且∠ACD=90°,求点D的坐标.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com