【题目】已知：如图，O是菱形ABCD对角线的交点，DE∥AC，CE∥BD，DE、CE交于点E． 
（1）猜想：四边形CEDO是什么特殊的四边形？
（2）试证明你的猜想．
【答案】
（1）解：猜想：四边形CEDO是矩形
（2）证明：∵DE∥AC，CE∥BD，
∴四边形OCED是平行四边形，
∵四边形ABCD是菱形，
∴AC⊥BD，
∴∠DOC=90°，
∴四边形OCED是矩形．
【解析】（1）猜想：四边形CEDO是矩形；（2）根据平行四边形的判定推出四边形是平行四边形，根据菱形性质求出∠DOC=90°，根据矩形的判定推出即可；
【考点精析】掌握平行线的性质和菱形的性质是解答本题的根本，需要知道两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补；菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半．
黎明文化寒假作业系列答案科目：初中数学 来源： 题型：
【题目】计算：（8x3﹣12x2﹣4x）÷（﹣4x）＝（ ）
A. ﹣2x2+3xB. ﹣2x2+3x+1C. ﹣2x2+3x﹣1D. 2x2+3x+1
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列不能进行平方差计算的是（ ）
A.（x+y）（﹣x﹣y）
B.（2a+b）（2a﹣b）
C.（﹣3x﹣y）（﹣y+3x）
D.（a2+b）（a2﹣b）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图所示，在平面直角坐标系
中，
.若点
是边
上的一个动点（与点
不重合），过点作
交
于点
.
（1）求点
的坐标；
（2）当
的周长与四边形
的周长相等时，求
的长；
（3）在
上是否存在点
，使得
为等腰直角三角形？若存在，请求出此时
的长；若不存在，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知关于x的一元二次方程
有实数根．
（1）求m的值；
（2）先作
的图象关于x轴的对称图形，然后将所作图形向左平移3个单位长度，再向上平移2个单位长度，写出变化后图象的解析式；
（3）在（2）的条件下，当直线y=2x+n（n≥m）与变化后的图象有公共点时，求
的最大值和最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
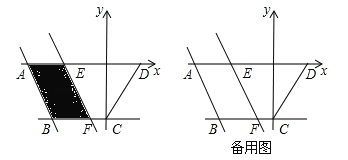
【题目】如图，在平面直角坐标系中，四边形ABCD的边AD在x轴上，点C在y轴的负半轴上，直线BC∥AD，且BC=3，OD=2，将经过A、B两点的直线l：y=﹣2x﹣10向右平移，平移后的直线与x轴交于点E，与直线BC交于点F，设AE的长为t（t≥0）．
（1）四边形ABCD的面积为 ；
（2）设四边形ABCD被直线l扫过的面积（阴影部分）为S，请直接写出S关于t的函数解析式；
（3）当t=2时，直线EF上有一动点，作PM⊥直线BC于点M，交x轴于点N，将△PMF沿直线EF折叠得到△PTF，探究：是否存在点P，使点T恰好落在坐标轴上？若存在，请求出点P的坐标；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com