Question

【题目】已知关于x的一元二次方程有实数根．

（1）求m的值；

（2）先作的图象关于x轴的对称图形，然后将所作图形向左平移3个单位长度，再向上平移2个单位长度，写出变化后图象的解析式；

（3）在（2）的条件下，当直线y=2x+n（n≥m）与变化后的图象有公共点时，求的最大值和最小值．

Answer 1

【答案】（1）1；（2）；（3）最大值为21，最小值为﹣4．

【解析】

试题分析：（1）由题意△≥0，列出不等式，解不等式即可；

（2）画出翻折．平移后的图象，根据顶点坐标即可写出函数的解析式；

（3）首先确定n的取值范围，利用二次函数的性质即可解决问题；

试题解析：（1）对于一元二次方程，△=（m+1）2﹣2（m2+1）=﹣m2+2m﹣1=﹣（m﹣1）2，∵方程有实数根，∴﹣（m﹣1）2≥0，∴m=1．

（2）由（1）可知= ，图象如图所示：

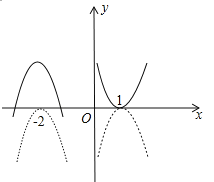
平移后的解析式为，即．

（3）由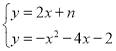消去y得到，由题意△≥0，∴36﹣4n﹣8≥0，∴n≤7，∵n≤m，m=1，∴1≤n≤7，令y′=n2﹣4n=（n﹣2）2﹣4，∴n=2时，y′的值最小，最小值为﹣4，n=7时，y′的值最大，最大值为21，∴的最大值为21，最小值为﹣4．