Question

【题目】已知：如图所示，在平面直角坐标系中，.若点是边上的一个动点（与点不重合），过点作交于点.

（1）求点的坐标；

（2）当的周长与四边形的周长相等时，求的长；

（3）在上是否存在点，使得为等腰直角三角形？若存在，请求出此时的长；若不存在，请说明理由.

Answer 1

【答案】（1）C（16，﹣12）；（2）；（3）存在，.

【解析】

试题分析：（1）如图1，过C作CH⊥OB于H，根据勾股定理得到BC=，根据三角形的面积公式得到CH=，由勾股定理得到OH=，则得到结论；

（2）∵根据相似三角形的性质得到，设CM=x，则CN=x，根据已知条件列方程即可得到结论；

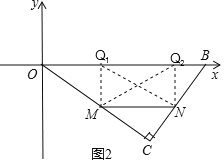
（3）如图2，由（2）知，当CM=x，则CN=x，MN=x，①当∠OMQ1=90°MN=MQ时，②当∠MNQ2=90°，MN=NQ2时，根据相似三角形的性质即可得到结论．

试题解析：（1）如图1，过C作CH⊥OB于H，

∵∠C=90°，OB=25，OC=20，∴BC=，

∵S△OBC=OBCH=OCBC，∴CH=，

∴OH=，∴C（16，﹣12）；

（2）∵MN∥OB，∴△CNM∽△COB，∴，

设CM=x，则CN=x，

∵△MCN的周长与四边形OMNB的周长相等，

∴CM+CN+MN=OM+MN+OB，即x+x+MN=20﹣x+mn+15﹣x+25，

解得：x=，∴CM=；

（3）如图2，由（2）知，当CM=x，则CN=x，MN=x，

①当∠OMQ1=90°MN=MQ时，

∵△OMQ∽△OBC，∴，

∵MN=MQ，∴，∴x=，

∴MN=x=×=；

②当∠MNQ2=90°，MN=NQ2时，

此时，四边形MNQ2Q1是正方形，

∴NQ2=MQ1=MN，∴MN=．