
【题目】如图,抛物线y=x2﹣2x﹣3与x轴交于A、B两点(点A在点B的左侧),直线l与抛物线交于A,C两点,其中点C的横坐标为2.
(1)求A,B两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点(P与A,C不重合),过P点作y轴的平行线交抛物线于点E,求△ACE面积的最大值;
(3)若直线PE为抛物线的对称轴,抛物线与y轴交于点D,直线AC与y轴交于点Q,点M为直线PE上一动点,则在x轴上是否存在一点N,使四边形DMNQ的周长最小?若存在,求出这个最小值及点M,N的坐标;若不存在,请说明理由.
(4)点H是抛物线上的动点,在x轴上是否存在点F,使A、C、F、H四个点为顶点的四边形是平行四边形?如果存在,请直接写出所有满足条件的F点坐标;如果不存在,请说明理由.

【答案】(1)y=﹣x﹣1;(2)△ACE的面积最大值为![]() ;(3)M(1,﹣1),N(
;(3)M(1,﹣1),N(![]() ,0);(4)满足条件的F点坐标为F1(1,0),F2(﹣3,0),F3(4+
,0);(4)满足条件的F点坐标为F1(1,0),F2(﹣3,0),F3(4+![]() ,0),F4(4﹣
,0),F4(4﹣![]() ,0).
,0).
【解析】
(1)令抛物线y=x2-2x-3=0,求出x的值,即可求A,B两点的坐标,根据两点式求出直线AC的函数表达式;
(2)设P点的横坐标为x(-1≤x≤2),求出P、E的坐标,用x表示出线段PE的长,求出PE的最大值,进而求出△ACE的面积最大值;
(3)根据D点关于PE的对称点为点C(2,-3),点Q(0,-1)点关于x轴的对称点为M(0,1),则四边形DMNQ的周长最小,求出直线CM的解析式为y=-2x+1,进而求出最小值和点M,N的坐标;
(4)结合图形,分两类进行讨论,①CF平行x轴,如图1,此时可以求出F点两个坐标;②CF不平行x轴,如题中的图2,此时可以求出F点的两个坐标.
(1)令y=0,解得![]() 或x2=3,
或x2=3,
∴A(﹣1,0),B(3,0);
将C点的横坐标x=2代入y=x2﹣2x﹣3得![]()
∴C(2,-3),
∴直线AC的函数解析式是![]()
(2)设P点的横坐标为x(﹣1≤x≤2),
则P、E的坐标分别为:P(x,﹣x﹣1),E(x,x2﹣2x﹣3),
∵P点在E点的上方,![]()
∴当![]() 时,PE的最大值
时,PE的最大值![]()
△ACE的面积最大值![]()
(3)D点关于PE的对称点为点C(2,﹣3),点Q(0,﹣1)点关于x轴的对称点为K(0,1),
连接CK交直线PE于M点,交x轴于N点,可求直线CK的解析式为![]() ,此时四边形DMNQ的周长最小,
,此时四边形DMNQ的周长最小,
最小值![]()
求得M(1,﹣1),![]()
(4)存在如图1,若AF∥CH,此时的D和H点重合,CD=2,则AF=2,
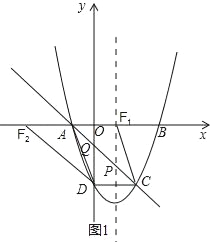
于是可得F1(1,0),F2(﹣3,0),
如图2,根据点A和F的坐标中点和点C和点H的坐标中点相同,

再根据|HA|=|CF|,
求出![]()
综上所述,满足条件的F点坐标为F1(1,0),F2(﹣3,0),![]() ,
,![]() .
.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】某校数学兴趣小组在一次数学课外活动中,随机抽查该校10名同学参加今年初中学业水平考试的体育成绩,得到结果如下表所示:

下列说法正确的是( )
A.这10名同学体育成绩的中位数为38分
B.这10名同学体育成绩的平均数为38分
C.这10名同学体育成绩的众数为39分
D.这10名同学体育成绩的方差为2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次实验中,小强把一根弹簧的上端固定,在其下端悬挂物体.下面是他测得的弹簧的长度y与所挂物体的质量石的一组对应值:
所挂物体的质量x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度y/cm | 20 | 22 | 24 | 26 | 25 | 30 |
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)填空:
①当所挂的物体为3kg时,弹簧长是____.不挂重物时,弹簧长是____.
②当所挂物体的质量为8kg(在弹簧的弹性限度范围内)时,弹簧长度是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.动点P从点A开始沿折线AC-CB-BA运动,点P在AC,CB,BA边上运动的速度分别为每秒3,4,5个单位.直线l从与AC重合的位置开始,以每秒![]() 个单位的速度沿CB方向移动,移动过程中保持l∥AC,且分别与CB,AB边交于E,F两点,点P与直线l同时出发,设运动的时间为t秒,当点P第一次回到点A时,点P和直线l同时停止运动.
个单位的速度沿CB方向移动,移动过程中保持l∥AC,且分别与CB,AB边交于E,F两点,点P与直线l同时出发,设运动的时间为t秒,当点P第一次回到点A时,点P和直线l同时停止运动.
(1)当t=5秒时,点P走过的路径长为_________;当t=_________秒时,点P与点E重合;
(2)当点P在AC边上运动时,连结PE,并过点E作AB的垂线,垂足为H. 若以C、P、E为顶点的三角形与△EFH相似,试求线段EH的值;
(3)当点P在折线AC-CB-BA上运动时,作点P关于直线EF的对称点Q.在运动过程中,若形成的四边形PEQF为菱形,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抓住梵净山文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
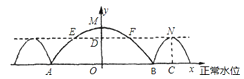
【题目】如图,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度![]() 米,顶点
米,顶点![]() 距水面
距水面![]() 米(即
米(即![]() 米),小孔顶点
米),小孔顶点![]() 距水面
距水面![]() 米(即
米(即![]() 米).当水位上涨刚好淹没小孔时,借助图中的直角坐标系,则此时大孔的水面宽度
米).当水位上涨刚好淹没小孔时,借助图中的直角坐标系,则此时大孔的水面宽度![]() 长为( )
长为( )
![]()
A. ![]() 米 B.
米 B. ![]() C.
C. ![]() 米 D.
米 D. ![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若正整数n使得在计算n+(n+1)+(n+2)的过程中,个数位上均不产生进为现象,则称n为“本位数”,例如2和30是“本位数”,而5和91不是“本位数”.现从所有大于0且小于100的“本位数”中,随机抽取一个数,抽到奇数的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,2)与(0,3)之间(不包括这两点),对称轴为直线x=2.下列结论:abc<0;②9a+3b+c>0;③若点M(![]() ,y1),点N(
,y1),点N(![]() ,y2)是函数图象上的两点,则y1<y2;④﹣
,y2)是函数图象上的两点,则y1<y2;④﹣![]() <a<﹣
<a<﹣![]() .其中正确结论有( )
.其中正确结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,直线CD与⊙O相切于点C,且与AB的延长线交于点E.点C是弧BF的中点.

(1)求证:AD⊥CD;
(2)若∠CAD=30°.⊙O的半径为3,一只蚂蚁从点B出发,沿着BE--EC--弧CB爬回至点B,求蚂蚁爬过的路程(π≈3.14,![]() ≈1.73,结果保留一位小数.)
≈1.73,结果保留一位小数.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com