练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．在活动课上，小明用一根长为10cm的小木棒，做一个边长为整数的等腰三角形，则小明可以拼出不同的符合条件的三角形最多有2个．

    分析 设腰长为x，则底边为10-2x，根据三角形三边关系可得到腰长可取的值，从而不难求得底边的长．

    解答 解：设腰长为x，则底边为10-2x．
    ∵10-2x-x＜x＜10-2x+x，
    ∴2.5＜x＜5，
    ∵三边长均为整数，
    ∴x可取的值为：3或4，
    ∴当腰长为3时，底边为4；当腰长为4时，底边为2．
    故答案为：2．

    点评 本题考查了等腰三角形的性质及三角形三边的关系，难度不大，关键是根据三角形三边关系求出x的取值范围．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

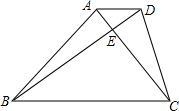    3．如图，在梯形ABCD中，AD∥BC，对角线AC与BD互相垂直，且BC-AD=4，cos∠DBC=0.8，AC=6．求BC的长及梯形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

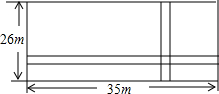    4．如图，在一块长35m，宽26m的矩形地面上修建同样宽的两条互相垂直的道路（两条道路各与矩形的一条边平行），剩余部分栽种花草，要使剩余部分的面积为850m2，道路的宽应该为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图，AB∥CD，BC与AD相交于点M，N是射线CD上的一点．若∠B=65°，∠MDN=135°，求：∠AMB的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

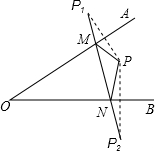    8．如图，点P为∠AOB内一点，分别作出P点关于OA、OB的对称点P1，P2，连接P1P2交OA于M，交OB于N，P1P2=20，则△PMN的周长为20．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．若$-\frac{1}{2}{x^3}{y^{n-1}}$与3xm+1y是同类项，则m=2，n=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

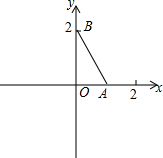    5．如图，在平面直角坐标系中，已知点A（1，0）和点B（0，2），点C在x轴上，若以A、B、C为顶点构成的三角形是等腰三角形，则满足条件的点C的坐标是（1-$\sqrt{5}$，0），（-1，0），（-$\frac{3}{2}$，0）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

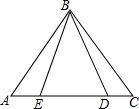    2．如图，如果△ABE≌△CBD，则它们的对应边分别是AB的对应边是CB，AE的对应边是CD，BE的对应边是BD；对应角分别是∠A的对应角是∠C，∠ABE的对应角是∠CBD，∠AEB的对应角是∠CDB；如果△BAD≌△BCE，则它们的对应边分别是AB的对应边是CB，AD的对应边是CE，BD的对应边是BE，对应角分别是∠ABD的对应角是∠CBE，∠ADB的对应角是∠CEB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．计算：
    （1）-2x+3y=-2x+3y．
    （2）2m+4m=6m．
    （3）2x2-3x2=-x2 
    （4）-2x-3y+5x=3x-3y
    （5）2xy-3x+5xy=-3xy-3x．

    查看答案和解析>>

    同步练习册答案