
【题目】下面是小立设计的“过直线外一点作这条直线的平行线”的尺规作图过程.
已知:如图1,直线l及直线l外一点A.
求作:直线AD,使得![]() .
.

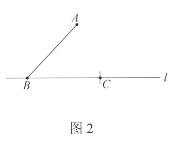
作法:如图2,
①在直线l上任取一点B,连接AB;
②以点B为圆心,AB长为半径画弧,交直线l于点C;
③分别以点A,C为圆心,AB长为半径画弧,两弧交于点D(不与点B重合);
④作直线AD.
所以直线AD就是所求作的直线.
根据小立设计的尺规作图过程,
(1).使用直尺和圆规,补全图形;(保留作图痕迹)
(2)2.完成下面的证明.(说明:括号里填推理的依据)
证明:连接CD.
∵![]() ,
,
∴四边形ABCD是___________(_________________).
∴![]() (_____________).
(_____________).
科目:初中数学 来源: 题型:
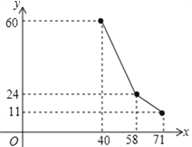
【题目】国家为支持大学生创业,提供小额无息贷款,学生王芳享受政策无息贷款36000元用来代理品牌服装的销售.已知该品牌服装进价每件40元,日销售y(件)与销售价x(元/件)之间的关系如图所示(实线),每天付员工的工资每人每天82元,每天应支付其它费用106元.
(1)求日销售y(件)与销售价x (元/件)之间的函数关系式;
(2)若暂不考虑还贷,当某天的销售价为48元/件时,收支恰好平衡(收入=支出),求该店员工人数;
(3)若该店只有2名员工,则该店至少需要多少天才能还清贷款,此时,每件服装的价格应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过两个确定点A、B,其中A为顶点,B为抛物线与y轴的交点.
(1)由抛物线的性质可知,该抛物线还经过一个确定点C,请写出找点C的方法(不要求画图);
(2)若A(1,4)、B(0,3),求抛物线的解析式.
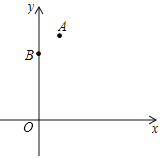
查看答案和解析>>
科目:初中数学 来源: 题型:
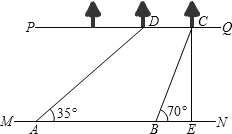
【题目】如图,河流的两岸PQ、MN互相平行,河岸PQ上有一排小树,已知相邻两树之间的距离CD=50米,某人在河岸MN的A处测得∠DAN=35°,然后沿河岸走了120米到达B处,测得∠CBN=70°.求河流的宽度CE(结果保留两个有效数字).(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荣庆公司计划从商店购买同一品牌的台灯和手电筒,已知购买一个台灯比购买一个手电筒多用20元,若用400元购买台灯和用160元购买手电筒,则购买台灯的个数是购买手电筒个数的一半.
(1)求购买该品牌一个台灯、一个手电筒各需要多少元?
(2)经商谈,商店给予荣庆公司购买一个该品牌台灯赠送一个该品牌手电筒的优惠,如果荣庆公司需要手电筒的个数是台灯个数的2倍还多8个,且该公司购买台灯和手电筒的总费用不超过670元,那么荣庆公司最多可购买多少个该品牌台灯?
查看答案和解析>>
科目:初中数学 来源: 题型:
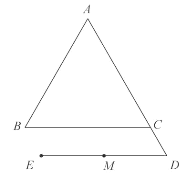
【题目】如图,在等边![]() 中,D为边AC的延长线上一点(
中,D为边AC的延长线上一点(![]() ),平移线段BC,使点C移动到点D,得到线段ED,M为ED的中点,过点M作ED的垂线,交BC于点F,交AC于点G.
),平移线段BC,使点C移动到点D,得到线段ED,M为ED的中点,过点M作ED的垂线,交BC于点F,交AC于点G.
(1)依题意补全图形;
(2)求证:![]() ;
;
(3)连接DF并延长交AB于点H,用等式表示线段AH与CG的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
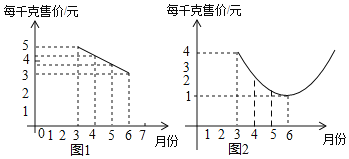
【题目】某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示(图1的图象是线段,图2的图象是抛物线)
(1)已知6月份这种蔬菜的成本最低,此时出售每千克的收益是多少元?(收益=售价﹣成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?简单说明理由.
(3)已知市场部销售该种蔬菜4、5两个月的总收益为22万元,且5月份的销售量比4月份的销售量多2万千克,求4、5两个月的销售量分别是多少万千克?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com