
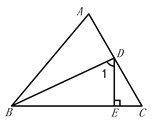
已知,在△ABC中三个内角的度数满足∠ABC:∠C:∠A=5:6:7,BD是△ABC的角平分线,DE是△DBC的高.
(1)求△ABC各内角的度数;
(2)求图中的度数.
科目:初中数学 来源:2018-2019学年北师大版七年级数学上册 第 2 章《有理数及其运算》经典题型单元测试卷 题型:单选题
如果水库的水位高于正常水位5m时,记作+5m,那么低于正常水位3m时,应记作( )
A. +3m B. ﹣3m C. + m D. ﹣5m
m D. ﹣5m
查看答案和解析>>
科目:初中数学 来源:北京市顺义区2018届九年级中考模拟试卷数学试卷 题型:解答题
如图,在矩形ABCD中,AB═2,AD= ,P是BC边上的一点,且BP=2CP.
,P是BC边上的一点,且BP=2CP.
(1)用尺规在图①中作出CD边上的中点E,连接AE、BE(保留作图痕迹,不写作法);
(2)如图②,在(1)的条体下,判断EB是否平分∠AEC,并说明理由;
(3)如图③,在(2)的条件下,连接EP并廷长交AB的廷长线于点F,连接AP,不添加辅助线,△PFB能否由都经过P点的两次变换与△PAE组成一个等腰三角形?如果能,说明理由,并写出两种方法(指出对称轴、旋转中心、旋转方向和平移距离)

查看答案和解析>>
科目:初中数学 来源:人教版数学八年级下册 第十七章 勾股定理 达标测试卷 题型:解答题
如图,某沿海城市A接到台风警报,在该城市正南方向260 km的B处有一台风中心,沿BC方向以15 km/h的速度向C移动,已知城市A到BC的距离AD=100 km,那么台风中心经过多长时间从B点移动到D点?如果在距台风中心30 km的圆形区域内都将受到台风的影响,正在D点休息的游人在接到台风警报后的几小时内撤离才可以免受台风的影响?

查看答案和解析>>
科目:初中数学 来源:人教版数学八年级下册 第十七章 勾股定理 达标测试卷 题型:填空题
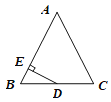
如图,△ABC中,AB=AC=13,BC=10,D为BC中点,DE⊥AB于E,则DE=_____.
查看答案和解析>>
科目:初中数学 来源:重庆市2018-2019学年八年级上学期期中考试数学试卷 题型:填空题
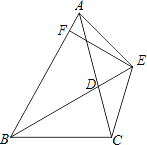
已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④BA+BC=2BF,其中正确的结论有________(填序号).
查看答案和解析>>
科目:初中数学 来源:重庆市2018-2019学年八年级上学期期中考试数学试卷 题型:单选题
三种不同类型的纸板的长宽如图所示,其中A类和C类是正方形,B类是长方形,现A类有1块,B类有4块,C类有5块. 如果用这些纸板拼成一个正方形,发现多出其中1块纸板,那么拼成的正方形的边长是( )
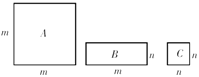
A. m+n B. 2m+2n C. 2m+n D. m+2n
查看答案和解析>>
科目:初中数学 来源:浙江省义乌市教育集团2018-2019学年八年级上学期期中考试数学试卷 题型:解答题
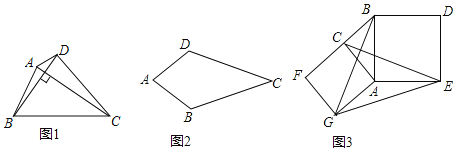
连接四边形不相邻两个顶点的线段叫做四边形的对角线,如图1,四边形ABCD中线段AC、线段BD就是四边形ABCD 的对角线.把对角线互相垂直的四边形叫做垂美四边形.
(1)概念理【解析】
如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.
(2)性质探究:试探索垂美四边形ABCD两组对边AB,CD的平方和与BC,AD的平方和之间的数量关系.
猜想结论:(要求用文字语言叙述)______
写出证明过程(先画出图形,写出已知、求证).
(3)问题解决:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com