
【题目】已知两个共一个顶点的等腰直角△ABC和等腰直角△CEF,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.
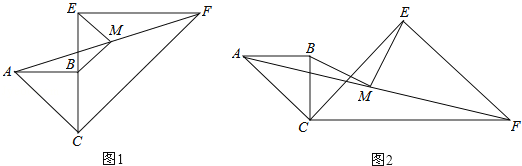
(1)如图1,当CB与CE在同一直线上时,求证:MB∥CF;
(2)如图1,若CB=a,CE=2a,求BM,ME的长;
(3)如图2,当∠BCE=45°时,求证:BM=ME.
【答案】(1)见解析(2)BM=ME==![]() a(3)见解析
a(3)见解析
【解析】
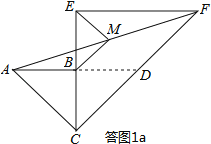
试题分析:(1)如答图1a所示,延长AB交CF于点D,证明BM为△ADF的中位线即可;
(2)如答图2a所示,作辅助线,推出BM、ME是两条中位线;
(3)如答图3a所示,作辅助线,推出BM、ME是两条中位线:BM=![]() DF,ME=
DF,ME=![]() AG;然后证明△ACG≌△DCF,得到DF=AG,从而证明BM=ME.
AG;然后证明△ACG≌△DCF,得到DF=AG,从而证明BM=ME.
(1)证明:如答图1a,延长AB交CF于点D,则易知△ABC与△BCD均为等腰直角三角形,
∴AB=BC=BD,
∴点B为线段AD的中点,
又∵点M为线段AF的中点,
∴BM为△ADF的中位线,
∴BM∥CF;
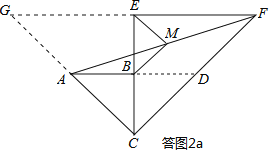
(2)如答图2a所示,延长AB交CF于点D,则易知△BCD与△ABC为等腰直角三角形,
∴AB=BC=BD=a,AC=CD=![]() a,
a,
∴点B为AD中点,又点M为AF中点,
∴BM=![]() DF.
DF.
分别延长FE与CA交于点G,则易知△CEF与△CEG均为等腰直角三角形,
∴CE=EF=GE=2a,CG=CF=2![]() a,
a,
∴点E为FG中点,又点M为AF中点,
∴ME=![]() AG.
AG.
∵CG=CF=2![]() a,CA=CD=
a,CA=CD=![]() a,
a,
∴AG=DF=![]() a,
a,
∴BM=ME=![]() ×
×![]() a=
a=![]() a.
a.
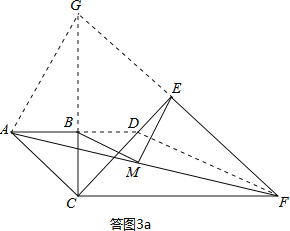
(3)如答图3a,延长AB交CE于点D,连接DF,则易知△ABC与△BCD均为等腰直角三角形,
∴AB=BC=BD,AC=CD,
∴点B为AD中点,又点M为AF中点,
∴BM=![]() DF,
DF,
延长FE与CB交于点G,连接AG,则易知△CEF与△CEG均为等腰直角三角形,
∴CE=EF=EG,CF=CG,
∴点E为FG中点,又点M为AF中点,
∴ME=![]() AG,
AG,
在△ACG与△DCF中,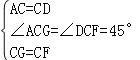 ,
,
∴△ACG≌△DCF(SAS),
∴DF=AG,
∴BM=ME.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】下列各式中去括号正确的是( )
A. a2-4(-a+1)= a2-4a﹣4 B. -(mn-1)+(m-n)=-mn-1+m-n
C. 5x-(2x-1)-x2= 5x-2x+1-x2 D. x2-2(2x-y+2)= x2-4x+y-2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. 对角线相等的四边形是矩形B. 对角线互相垂直的四边形是正方形
C. 平行四边形的对角线平分一组对角D. 矩形的对角线相等且互相平分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
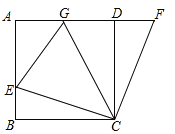
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了预测八年级男生“排球30秒”对墙垫球的情况,从本校八年级随机抽取了n名男生进行该项目测试,并绘制出如图的频数分布直方图,其中从左到右依次分为七个组(每组含最小值,不含最大值).根据统计图提供的信息解答下列问题:
(1)填空:n=50;这个样本数据的中位数落在第三组.
(2)若测试八年级男生“排球30秒”对墙垫球个数不低于10个为合格,根据统计结果,估计该校八年级500名男同学成绩合格的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初一所有学生将在大礼堂内参加2017年“元旦联欢晚会”,若每排坐30人,则有8人无座位;若每排坐31人,则空26个座位,则初一年级共有多少名学生?设大礼堂内共有x排座位,可列方程为______________________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com