
【题目】如图,P为∠AOB内一定点,M、N分别是射线OA、OB上一点,当△PMN周长最小时,∠OPM=50°,则∠AOB=( )
A.40°B.45°C.50°D.55°
【答案】A
【解析】
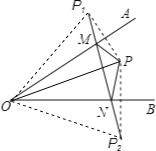
作P关于OA,OB的对称点P1,P2.连接OP1,OP2.则当M,N是P1P2与OA,OB的交点时,△PMN的周长最短,根据对称的性质可以证得:∠OP1M=∠OPM=50°,OP1=OP2=OP,根据等腰三角形的性质即可求解.
解:作P关于OA,OB的对称点P1,P2.连接OP1,OP2.则当M,N是P1P2与OA,OB的交点时,△PMN的周长最短,连接P1O、P2O,
∵PP1关于OA对称,
∴∠P1OP=2∠MOP,OP1=OP,P1M=PM,∠OP1M=∠OPM=50°
同理,∠P2OP=2∠NOP,OP=OP2,
∴∠P1OP2=∠P1OP+∠P2OP=2(∠MOP+∠NOP)=2∠AOB,OP1=OP2=OP,
∴△P1OP2是等腰三角形.
∴∠OP2N=∠OP1M=50°,
∴∠P1OP2=180°﹣2×50°=80°,
∴∠AOB=40°,
故选:A.


科目:初中数学 来源: 题型:
【题目】如图,小河边有两个村庄A、B,要在河边建一自来水厂向A村与B村供水。
(1)若要使水厂到A、B村的距离相等,则应选择在哪建厂?
(2)若要使水厂到A、B村的水管最省料,应建在什么地方?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,D为AB上一点,过D点作AB垂线,交AC于E,交BC的延长线于F.

(1)∠1与∠B有什么关系?说明理由.
(2)若BC=BD,请你探索AB与FB的数量关系,并且说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,BE交AD于点F,交AC于点E,若BE平分∠ABC,试判断△AEF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分)阅读材料:分解因式:![]()
解:![]()
=![]()
=![]()
=![]()
=![]()
=![]() ,
,
此种方法抓住了二次项和一次项的特点,然后加一项,使三项成为完全平方式,我们把这种分解因式的方法叫配方法.
(1)用上述方法分解因式:![]() ;
;
(2)无论![]() 取何值,代数式
取何值,代数式![]() 总有一个最小值,请尝试用配方法求出当
总有一个最小值,请尝试用配方法求出当![]() 取何值时代数式的值最小,并求出这个最小值.
取何值时代数式的值最小,并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高港花卉中心销售一批兰花,每盆进价![]() 元,售价为
元,售价为![]() 元,平均每天可售出
元,平均每天可售出![]() 盆.为了扩大销量,该店决定适当降价.据调查,每盆兰花每降价
盆.为了扩大销量,该店决定适当降价.据调查,每盆兰花每降价![]() 元,每天可多售出
元,每天可多售出![]() 盆.
盆.
![]() 要使得每天利润达到
要使得每天利润达到![]() 元,则每盆兰花售价应定为多少元?
元,则每盆兰花售价应定为多少元?
![]() 如果该店每天兰花的进货成本不超过
如果该店每天兰花的进货成本不超过![]() 元,要使得每天利润达到
元,要使得每天利润达到![]() 元,则每盆兰花售价应定为多少元?
元,则每盆兰花售价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“五一”劳动节期间,某商场为吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成20份),并规定:顾客每购物满200元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准标有数字的区域(未标数字的视为0),则顾客就可以分别获得该区域相应数字的返金券,凭返金券可以在该商场继续购物.若顾客不愿意转转盘,则每购物满200元可享受九五折优惠.
(1)写出转动一次转盘获得返金券的概率;
(2)转转盘和直接享受九五折优惠,你认为哪种方式对顾客更合算?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com