
【题目】已知:在△ABC中,AC=BC,∠ACB=90°,过点C作CD⊥AB于点D,点E是AB边上一动点(不含端点A、B),连接CE,过点B作CE的垂线交直线CE于点F,交直线CD于点G(如图①).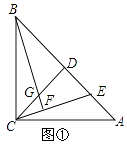
(1)求证:AE=CG;
(2)若点E运动到线段BD上时(如图②),试猜想AE、CG的数量关系是否发生变化,请直接写出你的结论;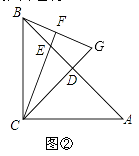
(3)过点A作AH垂直于直线CE,垂足为点H,并交CD的延长线于点M(如图③),找出图中与BE相等的线段,并证明.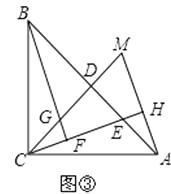
【答案】
(1)解:∵AC=BC,
∴∠ABC=∠CAB.
∵∠ACB=90°,
∴∠ABC=∠A=45°,∠ACE+∠BCE=90°.
∵BF⊥CE,
∴∠BFC=90°,
∴∠CBF+∠BCE=90°,
∴∠ACE=∠CBF
∵在RT△ABC中,CD⊥AB,AC=BC,
∴∠BCD=∠ACD=45°
∴∠A=∠BCD.
在△BCG和△ACE中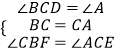 ,
,
∴△BCG≌△ACE(ASA),
∴AE=CG
(2)解:不变.AE=CG.
理由:∵AC=BC,
∴∠ABC=∠CAB.
∵∠ACB=90°,
∴∠ABC=∠A=45°,∠ACE+∠BCE=90°.
∵BF⊥CE,
∴∠BFC=90°,
∴∠CBF+∠BCE=90°,
∴∠ACE=∠CBF
∵在RT△ABC中,CD⊥AB,AC=BC,
∴∠BCD=∠ACD=45°
∴∠A=∠BCD.
在△BCG和△ACE中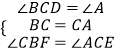 ,
,
∴△BCG≌△ACE(ASA),
∴AE=CG
(3)解:BE=CM,
:∵AC=BC,
∴∠ABC=∠CAB.
∵∠ACB=90°,
∴∠ABC=∠A=45°,∠ACE+∠BCE=90°.
∵AH⊥CE,
∴∠AHC=90°,
∴∠HAC+∠ACE=90°,
∴∠BCE=∠HAC.
∵在RT△ABC中,CD⊥AB,AC=BC,
∴∠BCD=∠ACD=45°
∴∠ACD=∠ABC.
在△BCE和△CAM中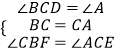 ,
,
∴△BCE≌△CAM(ASA),
∴BE=CM
【解析】(1)要证AE=CG,需证它们所在的三角形全等,据等腰直角三角形的性质可以得出∠BCD=∠ACD=45°,根据直角三角形的三角形的性质就可以得出∠CBF=∠ACE,由ASA就可以得出△BCG≌△CAE;(2)借鉴(1)的思路方法,仍运用全等法,根据等腰直角三角形的性质可以得出∠BCD=∠ACD=45°,根据直角三角形的三角形的性质就可以得出∠CBF=∠ACE,由ASA就可以得出△BCG≌△CAE,就可以得出结论;(3)借鉴(2)的思路,根据等腰直角三角形的性质可以得出∠BCD=∠ACD=45°,根据直角三角形的三角形的性质就可以得出∠CBF=∠ACE,由ASA就可以得出△BCG≌△CAE,就可以得出结论;F,交直线CD于点G.


科目:初中数学 来源: 题型:
【题目】探索与计算:
在△ABC中,BE⊥AC于点E,CD⊥AB于点D,连接DE.
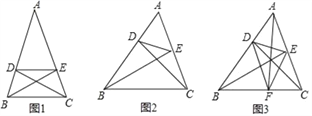
(1)如图1,若∠A=45°,AB=AC,BC=4,求DE的长.
(2)如图2,若∠A=60°,AB与AC不相等,BC=4,求DE的长.
猜想与证明:
(3)根据(1)(2)所求出的结果,猜想DE、BC以及∠A之间的数量关系,并证明.
拓展与应用:
(4)如图3,在△ABC中,AB=BC=5,AC=2![]() ,BE⊥AC于点E,CD⊥AB于点D,AF⊥BC于点F,求△DEF的周长.
,BE⊥AC于点E,CD⊥AB于点D,AF⊥BC于点F,求△DEF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,BD=CE.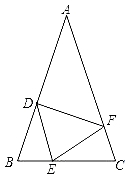
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;
(3)△DEF可能是等腰直角三角形吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB以O为圆心,以任意长为半径作弧,分别交OA、OB于F、E两点,再分别以E、F为圆心,大于 ![]() EF长为半径作圆弧,两条圆弧交于点P,作射线OP,过点F作FD∥OB交OP于点D.
EF长为半径作圆弧,两条圆弧交于点P,作射线OP,过点F作FD∥OB交OP于点D.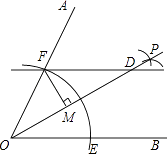
(1)若∠OFD=116°,求∠DOB的度数;
(2)若FM⊥OD,垂足为M,求证:△FMO≌△FMD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com