
����Ŀ��̽������㣺
�ڡ�ABC�У�BE��AC�ڵ�E��CD��AB�ڵ�D������DE��
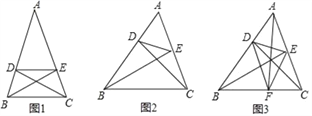
��1����ͼ1������A=45�㣬AB=AC��BC=4����DE�ij���
��2����ͼ2������A=60�㣬AB��AC����ȣ�BC=4����DE�ij���
������֤����
��3�����ݣ�1����2��������Ľ��������DE��BC�Լ���A֮���������ϵ����֤����
��չ��Ӧ�ã�
��4����ͼ3���ڡ�ABC�У�AB=BC=5��AC=2![]() ��BE��AC�ڵ�E��CD��AB�ڵ�D��AF��BC�ڵ�F�����DEF���ܳ���
��BE��AC�ڵ�E��CD��AB�ڵ�D��AF��BC�ڵ�F�����DEF���ܳ���
���𰸡�(1) DE=2![]() ��(2) DE =2��(3) DE=BCcosA,֤��������;(4) ��DEF���ܳ�=
��(2) DE =2��(3) DE=BCcosA,֤��������;(4) ��DEF���ܳ�=![]() .
.
�������������������1�����ݵ���ֱ�������ε����ʵõ�AE=BE=![]() AB���������������ε��ж������õ���ADE�ס�ABC���������������ε����ʼ��㣻
AB���������������ε��ж������õ���ADE�ס�ABC���������������ε����ʼ��㣻
��2������ֱ�������ε����ʵõ�AE=![]() AB��AD=
AB��AD=![]() AC���������������ε��ж������õ���ADE�ס�ACB���������������ε����ʼ��㣻
AC���������������ε��ж������õ���ADE�ס�ACB���������������ε����ʼ��㣻
��3���������ҵĸ�����������ε��ж������ʽ��
��4�����ݣ�3���Ľ��ۡ������ε������ʽ�����ɶ������㼴�ɣ�
���������
��1����BE��AC����A=45�㣬
��AE=BE=![]() AB��
AB��
ͬ����AD=CD=![]() AC��
AC��
��AB=AC��
��AE=AD��
��![]() =
=![]() ������A=��A��
������A=��A��
���ADE�ס�ABC��
��![]() =
=![]() =
=![]() ��
��
��DE=2![]() ��
��
��2����BE��AC����A=60�㣬
��AE=![]() AB��
AB��
ͬ����AD=![]() AC��
AC��
��![]() =
=![]() ������A=��A��
������A=��A��
���ADE�ס�ACB��
��![]() =
=![]() ��
��
��DE=![]() BC=2��
BC=2��
��3�����룺DE=BCcosA��
֤������BE��AC��
��cosA=![]() ��
��
��AE=ABcosA��
ͬ����AD=ACcosA��
����ADE�ס�ACB��
��![]() =cosA��
=cosA��
��DE=BCcosA��
��4����AB=BC=5��AC=2![]() ��BE��AC��
��BE��AC��
��AE=EC=![]() ��
��
�ɹ��ɶ����ã�BE=![]() =2
=2![]() ��
��
��BC��AF=AC��BE��
��AF=4��
�ɹ��ɶ����ã�BF=3��
��cos��ABC=![]() =
=![]() ��cos��ACB=cos��BAC=
��cos��ACB=cos��BAC=![]() ��
��
��EF=DE=ABcos��ACB=![]() ��DF=ACcos��ABC=
��DF=ACcos��ABC=![]() ��
��
���DEF���ܳ�=DE+EF+DF=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������߶��ܹ��������ε��ǣ�������
A��2��2��4 B��3��4��5 C��1��2��3 D��2��3��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ������A(5��6)���B����x��Գ������B������Ϊ( )
A. (5��6) B. (��5����6) C. (��5��6) D. (5����6)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ǹ������¶��壺��һ���ı��ε������Խ�����ȣ��������ı���Ϊ�ȶԽ����ı��Σ������������⣺
��1��д������ѧ���������ı������ǵȶԽ����ı��ε�����ͼ�ε����ƣ�
��2��̽�������ȶԽ����ı����������Խ����������Ϊ60��ʱ�����60������Ե�����֮��������һ���Խ��ߵĴ�С��ϵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijУ��ѧ¥AB�ĺ�����һ�칫¥CD�������������ļн���22��ʱ����ѧ¥�ڽ������ǽ�����¸�3��Ӱ��CE���������������ļн���45��ʱ����ѧ¥��A�ڵ����ϵ�Ӱ��F��ǽ��C��30�ľ��루B��F��C��һ��ֱ���ϣ�����Ҫ��A��E֮���һЩ���죬��A��E֮��ľ��룮���ο����ݣ�sin22���![]() ��cos22���
��cos22���![]() ��tan22���
��tan22���![]() ����ȷ��0.1m��
����ȷ��0.1m��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����x2+6x+m2��һ����ȫƽ��ʽ����m��ֵΪ�� ��
A. 3 B. -3 C. ��3 D. ���϶�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x2+x��1����px+2���ij˻��У�����x2���p��ֵ�ǣ�������
A.1
B.0
C.��1
D.��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�н����п�����ʵ��������ԣ�����ѧ����ǩ��ʽ�����Լ��Ŀ������ݣ��涨ÿλ������������������ʵ�飨��ֽǩA��B��C��ʾ����������ѧ���飨��ֽǩD��E��F��ʾ���и���ȡһ��ʵ��������п��ԣ�С���ڿ�����ֽǩ������£��ֱ���и������ȡһ�������б�����״ͼ�ķ�����С�ճ鵽����ʵ��B�ͻ�ѧʵ��F�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ڡ�ABC�У�AC=BC����ACB=90�㣬����C��CD��AB�ڵ�D����E��AB����һ���㣨�����˵�A��B��������CE������B��CE�Ĵ��߽�ֱ��CE�ڵ�F����ֱ��CD�ڵ�G����ͼ�٣���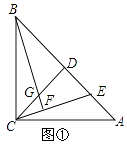
��1����֤��AE=CG��
��2������E�˶����߶�BD��ʱ����ͼ�ڣ����Բ���AE��CG��������ϵ�Ƿ����仯����ֱ��д����Ľ��ۣ�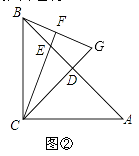
��3������A��AH��ֱ��ֱ��CE������Ϊ��H������CD���ӳ����ڵ�M����ͼ�ۣ����ҳ�ͼ����BE��ȵ��߶Σ���֤����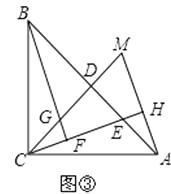
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com