
【题目】在平面直角坐标系中,点A、B、C、D是坐标轴上的点且点C坐标是(0,﹣1),AB=5,点(a,b)在如图所示的阴影部分内部(不包括边界),已知OA=OD=4,则a的取值范围是( ) 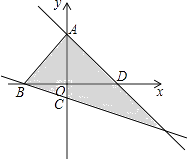
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:∵AB=5,OA=4,
∴OB= ![]() =3,
=3,
∴点B(﹣3,0).
∵OA=OD=4,
∴点A(0,4),点D(4,0).
设直线AD的解析式为y=kx+b,
将A(0,4)、D(4,0)代入y=kx+b,
![]() ,解得:
,解得: ![]() ,
,
∴直线AD的解析式为y=﹣x+4;
设直线BC的解析式为y=mx+n,
将B(﹣3,0)、C(0,﹣1)代入y=mx+n,
![]() ,解得:
,解得: 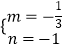 ,
,
∴直线BC的解析式为y=﹣ ![]() x﹣1.
x﹣1.
联立直线AD、BC的解析式成方程组,
 ,解得:
,解得: 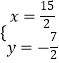 ,
,
∴直线AD、BC的交点坐标为( ![]() ,﹣
,﹣ ![]() ).
).
∵点(a,b)在如图所示的阴影部分内部(不包括边界),
∴﹣3<a< ![]() .
.
故选D.
【考点精析】通过灵活运用不等式的解集在数轴上的表示,掌握不等式的解集可以在数轴上表示,分三步进行:①画数轴②定界点③定方向.规律:用数轴表示不等式的解集,应记住下面的规律:大于向右画,小于向左画,等于用实心圆点,不等于用空心圆圈即可以解答此题.


科目:初中数学 来源: 题型:
【题目】(本题8分)如图1,平行四边形ABCD中,点O是对角线AC的中点,EF过点O,与AD,BC分别相交于点E,F,GH过点O,与AB,CD分别相交于点G,H,连接EG,FG,FH,EH.

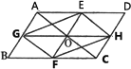
(1)求证:四边形EGFH是平行四边形;
(2)如图2,若EF//AB,GH//BC,在不添加任何辅助线的情况下,请直接写出图2中与四边形AGHD面积相等的所有平行四边形(四边形AGHD除外).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.

求证:(1)△AFD≌△CEB.(2)四边形ABCD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点
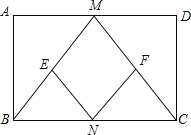
(1)求证:△ABM≌△DCM
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD:AB= _时,四边形MENF是正方形(只写结论,不需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场在一楼与二楼之间装有一部自动扶梯,以均匀的速度向上行驶,一男孩与一女孩同时从自动扶梯上走到二楼(扶梯本身也在行驶).如果二人都做匀速运动,且男孩每分钟走动的级数是女孩的两倍.又已知男孩走了27级到达顶部,女孩走了18级到达顶部(二人每步都只跨1级).求扶梯有多少级?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等的三角形的对数是______ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习三角形中位线的性质时,小亮对课本给出的解决办法进行了认真思考:
课本研究三角形中位线性质的方法 |

请你利用小亮的发现解决下列问题:
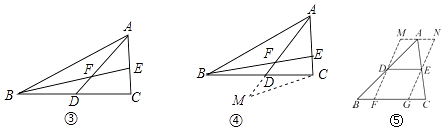
(1)如图③,AD是△ABC的中线,BE交AC于点E,交AD于点F,且AE=EF,求证:AC=BF.
请你帮助小亮写出辅助线作法并完成论证过程:
(2)解决问题:如图⑤,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线.过点D,E作DF∥EG,分别交BC于点F,G,过点A作MN∥BC,分别与FD,GE的延长线交于点M,N,则四边形MFGN周长的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
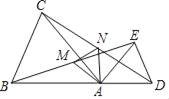
【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在同一条直线上,M,N分别为BE,CD的中点.
(1)求证:△ABE≌ACD;
(2)判断△AMN的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1 , 另两张直角三角形纸片的面积都为S2 , 中间一张正方形纸片的面积为S3 , 则这个平行四边形的面积一定可以表示为( ) 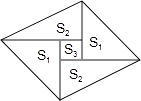
A.4S1
B.4S2
C.4S2+S3
D.3S1+4S3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com