
【题目】如图,在单位长度为1的数轴上有,A、B、C、D四个点,点A、C表示的有理数互为相反数.
(1)请在数轴上标出点A、B、C、D上方标出它们所表示的有理数;
(2)A、C两点间的距离AC= ,B、D两点间距离BD= ;
(3)设点P在数轴表示的有理数是x,借助数轴解答下列问题:式子|x-4|表示点P与有理数 所对应的点之间的距离:|x+1|表示点P与有理数 所对应的点之间的距离;
(4)①通过观察可以发现,可以利用绝对值来表示两个有理数在效轴上所对应的点之间的距离,如果数轴上点M表示的有理数是x,点N表示的有理数是y,那么M N两点间的距离可以表示为 .
②式子|x-3|+|x+3|的最小值是 .
![]()
【答案】(1)见解析;(2)6,5;(3)4,-1;(4)①MN=|x-y|,②6.
【解析】
(1)根据图示,点A、C之间的距离是6,据此求出点A、C表示的数是多少,即可求出点B和D表示的数是多少,并画数轴即可;
(2)直接由两点的坐标之差可得结论;
(3)根据绝对值的几何意义,进行解答;
(4)①在数轴上M、N两点之间的距离MN=|x-y|,依此即可求解;
②根据数轴上|x-3|+|x+3|的几何意义,进行解答.
解:(1)∵点A、C表示的两个数互为相反数,点A、C之间的距离是6,
∴点C表示的数是3,A表示的数是-3,
∴点B表示的数是-1,点D表示的数是4;
如图所示:

(2)由数轴得:A、C两点间的距离AC=6,B、D两点间距离BD=4-(-1)=5;
故答案为:6,5;
(3)式子|x-4|表示点P与有理数4所对应的点之间的距离:|x+1|表示点P与有理数-1所对应的点之间的距离;
(4)①在数轴上M、N两点之间的距离MN=|x-y|,
②式子|x-3|表示点P与有理数3所对应的点之间的距离:|x+3|表示点P与有理数-3所对应的点之间的距离;在数轴上|x-3|+|x+3|的几何意义是:表示有理数x的点到-3及到3的距离之和,所以当-3≤x≤3时,它的最小值为6;


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】先阅读下面的材料,再解答后面的各题:
现代社会对保密要求越来越高,密码正在成为人们生活的一部分.有一种密码的明文(真实文)按计算机键盘字母排列分解,其中Q,W,E,……,N,M这26个字母依次对应1,2,3,……,25,26这26个自然数(见下表).
Q | W | E | R | T | Y | U | I | O | P | A | S | D |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
F | G | H | J | K | L | Z | X | C | V | B | N | M |
14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
给出一个变换公式:

将明文转成密文,如:![]() ,即R变为L;
,即R变为L;![]() ,即A变为S.
,即A变为S.
将密文转换成明文,如:![]() ,即X变为P;13
,即X变为P;13![]() 3×(13-8)-1=14,即D变为F.
3×(13-8)-1=14,即D变为F.
(1)按上述方法将明文NET译为密文.
(2)若按上方法将明文译成的密文为DWN,请找出它的明文.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O在直线MN上,过点O作射线OP,使∠MOP=130°,现将一块直角三角板的直角顶点始终放在点O处.

(1)如图①,当三角板的一边OA在射线OM上,另一边OB在直线MN的上方时,∠POB的度数 是 ;
(2)若将三角板绕点O旋转至图②所示的位置,此时OB恰好平分∠PON,则∠BOP 的度数为 ;∠AOM 的度数为 ;
(3)若将三角板绕点O旋转至图③所示位置,此时OA在∠PON 的内部,
①若 OP 所在的直线平分∠MOB,则∠POA 的度数为 ;
②∠BON-∠POA的度数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将下列各数填在相应的集合里。
-3.8, -20%, 4.3, -∣-![]() ∣,
∣, ![]() , 0, -(-
, 0, -(-![]() ),
), ![]()
整数集合:{ … };
分数集合:{ … };
正数集合:{ … };
负数集合:{ … }.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连接CE、CF,EF,则以下四个结论一定正确的是:①△CDF≌△EBC;②∠CDF=∠EAF;③△ECF是等边△;④CG⊥AE( )
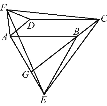
A. 只有①② B. 只有①②③ C. 只有③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】原来公园有一个半径为 1 m 的苗圃,现在准备扩大面积,设当扩大后的半径为x m时,则增加的环形的面积为y m 2 .
(1)写出y与x的函数关系式;
(2)当半径增大到多少时面积增大1倍;
(3)试猜测半径是多少时,面积是原来的3、4、5、…倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,sinA=![]() ,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
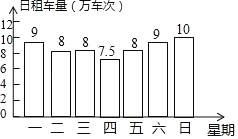
【题目】摩拜公司为了调查在某市投放的共享单车使用情况,对4月份第一个星期中每天摩拜单车使用情况进行统计,结果如图所示.
(1)求这一个星期每天单车使用情况的众数、中位数和平均数;
(2)用(1)中的结果估计4月份一共有多少万车次?
(3)摩拜公司在该市共享单车项目中共投入9600万元,估计本年度共租车3200万车次,若每车次平均收入租车费0.75元,请估计本年度全年租车费收入占总投入的百分比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com