
【题目】已知点O在直线MN上,过点O作射线OP,使∠MOP=130°,现将一块直角三角板的直角顶点始终放在点O处.

(1)如图①,当三角板的一边OA在射线OM上,另一边OB在直线MN的上方时,∠POB的度数 是 ;
(2)若将三角板绕点O旋转至图②所示的位置,此时OB恰好平分∠PON,则∠BOP 的度数为 ;∠AOM 的度数为 ;
(3)若将三角板绕点O旋转至图③所示位置,此时OA在∠PON 的内部,
①若 OP 所在的直线平分∠MOB,则∠POA 的度数为 ;
②∠BON-∠POA的度数为 .
【答案】(1)40゜;(2)25゜,65゜;(3)①40゜;②40゜.
【解析】
(1)根据∠POB=∠MOP-∠AOB代入数据即可求出结论;
(2)根据∠PON=180°-∠MOP可算出∠PON的度数,根据OB平分∠PON即可求出∠POB的度数,再通过角的计算可得出∠AOP=60°,结合∠MOP=130°即可得出∠AOM;
(3)①根据OP 所在的直线平分∠MOB,可得出∠MOB=100°,从而可求出∠BON=80°,根据∠BOA=90°求出∠AON=10°,根据∠POA=∠PON-∠AON可得结论;
②设∠AON=x°,则∠BON=90°-x°,∠POA=50°-x°,二者做差即可得出结论.
(1)∠POB=∠MOP-∠AOB=130°-90°=40°.
(2)∵∠MON是平角,∠MOP=130゜,
∴∠PON=∠MON-∠MOP=180゜-130゜=50゜
∵OB 平分∠PON,
∴∠BOP=![]() ∠PON=25゜
∠PON=25゜
∵∠AOB=90゜,
∴∠AOP=∠AOB-∠BOP=90゜-25゜=65゜
∴∠MOA=∠MOP-∠AOP=130゜-65゜=65゜;
(3)①如图,OE是PO的延长线,

∵∠MOP=130゜
∴∠MOE=50゜
∵OE是∠MOB的平分线,
∴∠MOB=100゜,
∴∠BON=80゜
∵∠AOB=90゜
∴∠AON=∠AOB-∠BON=90゜-80゜=10゜
∴∠POA=∠PON-∠AON=50゜-10゜=40゜;
②设∠AON=x°,则∠BON=90°-x°,∠POA=50°-x°,
∴∠BON-∠POA=(90°-x°)-(50°-x°)=40°.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:
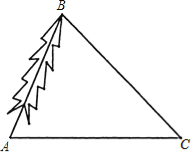
【题目】为了对一棵倾斜的古杉树AB进行保护,需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=24m,∠BAC=66.5°,求这棵古杉树AB的长度.(结果取整数)
参考数据:![]() ≈1.41,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30.
≈1.41,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点A、B、O在数轴上对应的数为a、b、0,且满足|a+8|+(b﹣12)2=0,点M、N分别从O、B出发,同时向左匀速运动,M的速度为1个单位长度每秒,N的速度为3个单位长度每秒,A、B之间的距离定义为:AB=|a﹣b|.
(1)直接写出OA= .OB= ;
(2)设运动的时间为t秒,当t为何值时,恰好有AN=2AM;
(3)若点P为线段AM的中点,Q为线段BN的中点,M、N在运动的过程中,PQ+MN的长度是否发生变化?若不变,请说明理由,若变化,当t为何值时,PQ+MN有最小值?最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于两数a和b,给定一种运算 “⊕”: a⊕b=a+b-ab, 则在下列等式中:①a⊕b=b⊕a;②a⊕0=a;③(a⊕b) ⊕c= a⊕(b⊕c) 正确的有___________ (填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在单位长度为1的数轴上有,A、B、C、D四个点,点A、C表示的有理数互为相反数.
(1)请在数轴上标出点A、B、C、D上方标出它们所表示的有理数;
(2)A、C两点间的距离AC= ,B、D两点间距离BD= ;
(3)设点P在数轴表示的有理数是x,借助数轴解答下列问题:式子|x-4|表示点P与有理数 所对应的点之间的距离:|x+1|表示点P与有理数 所对应的点之间的距离;
(4)①通过观察可以发现,可以利用绝对值来表示两个有理数在效轴上所对应的点之间的距离,如果数轴上点M表示的有理数是x,点N表示的有理数是y,那么M N两点间的距离可以表示为 .
②式子|x-3|+|x+3|的最小值是 .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是________(填A或B或C)
A.a2-2ab+b2=(a-b)2
B.a2-b2=(a+b)(a-b)
C.a2+ab=a(a+b)
(2)应用你从(1)中选出的等式,完成下列各题:
①已知x2-4y2=12,x+2y=4,求x-2y的值
②计算:(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )…(1-
)…(1-![]() )(1-
)(1-![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com