
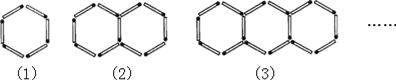
【题目】用火柴棒按如图所示的方式摆图形,按照这样的规律继续摆下去,则第100个图形需要火柴棒________根.
【答案】501
【解析】
仔细观察图形,数一数①、②、③图中每个图形各有几个六边形,有几根火柴棒公用,其由几根火柴棒组成;则根据规律可得第100个图形由100个六边形组成,有99根火柴棒公用即可解答.
仔细观察图形可知:
图形①为1个六边形,有1-1=0根火柴棒公用,其由6×1-0=6根火柴棒组成;
图形②为2个六边形,有2-1=1根火柴棒公用,其由6×2-1=11根火柴棒组成;
图形③为3个六边形,有3-1=2根火柴棒公用,其由6×3-2=16根火柴棒组成;
……
可猜想:第10个图形由100个六边形,有100-1=99根公用,其由6×100-99=501根火柴棒组成;
故第100个图形需火柴棒501根.
故答案为:501.


科目:初中数学 来源: 题型:
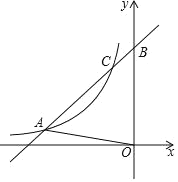
【题目】如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=![]() (m≠0,x<0)的图象交于点A(﹣3,1)和点C,与y轴交于点B,△AOB的面积是6.
(m≠0,x<0)的图象交于点A(﹣3,1)和点C,与y轴交于点B,△AOB的面积是6.
(1)求反比例函数与一次函数的解析式;
(2)当x<0时,比较y1与y2的大小;
(3)若点P(x,y)也在反比例函数y2=![]() 的图象上,当﹣4≤x≤﹣
的图象上,当﹣4≤x≤﹣![]() 时,求函数值y的取值范围.
时,求函数值y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,巨型广告牌AB背后有一看台CD,台阶每层高0.3米,且AC=17米,现有一只小狗睡在台阶的FG这,层上晒太阳,设太阳光线与水平地面的夹角为α,当α=60°时,测得广告牌AB在地面上的影长AE=10米,过了一会,当α=45°,问小狗在FG这层是否还能晒到太阳?请说明理由(![]() 取1.73).
取1.73).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的材料,再解答后面的各题:
现代社会对保密要求越来越高,密码正在成为人们生活的一部分.有一种密码的明文(真实文)按计算机键盘字母排列分解,其中Q,W,E,……,N,M这26个字母依次对应1,2,3,……,25,26这26个自然数(见下表).
Q | W | E | R | T | Y | U | I | O | P | A | S | D |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
F | G | H | J | K | L | Z | X | C | V | B | N | M |
14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
给出一个变换公式:

将明文转成密文,如:![]() ,即R变为L;
,即R变为L;![]() ,即A变为S.
,即A变为S.
将密文转换成明文,如:![]() ,即X变为P;13
,即X变为P;13![]() 3×(13-8)-1=14,即D变为F.
3×(13-8)-1=14,即D变为F.
(1)按上述方法将明文NET译为密文.
(2)若按上方法将明文译成的密文为DWN,请找出它的明文.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形OABC顶点B的坐标为(8,3),定点D的坐标为(12,0),动点P从点O出发,以每秒2个单位长度的速度沿x轴的正方向匀速运动,动点Q从点D出发,以每秒1个单位长度的速度沿x轴的负方向匀速运动,PQ两点同时运动,相遇时停止.在运动过程中,以PQ为斜边在x轴上方作等腰直角三角形PQR.设运动时间为t秒.
(1)当t= 时,△PQR的边QR经过点B;
(2)设△PQR和矩形OABC重叠部分的面积为S,求S关于t的函数关系式;
(3)如图2,过定点E(5,0)作EF⊥BC,垂足为F,当△PQR的顶点R落在矩形OABC的内部时,过点R作x轴、y轴的平行线,分别交EF、BC于点M、N,若∠MAN=45°,求t的值.
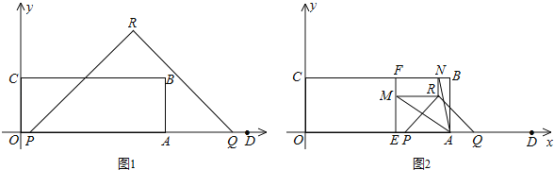
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D。连结OD,作BE⊥CD于点E,交半圆O于点F。已知CE=12,BE=9,
(1)求证:△COD∽△CBE;
(2)求半圆O的半径的长

查看答案和解析>>
科目:初中数学 来源: 题型:
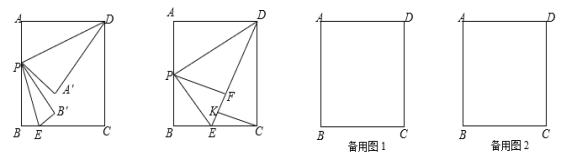
【题目】如图,在矩形ABCD中,AB=8,BC=6,点P、点E分别是边AB、BC上的动点,连结DP、PE.将△ADP与△BPE分别沿DP与PE折叠,点A与点B分别落在点A′,B′处.
(1) 当点P运动到边AB的中点处时,点A′与点B′重合于点F处,过点C作CK⊥EF于K,求CK的长;
(2) 当点P运动到某一时刻,若P,A',B'三点恰好在同一直线上,且A'B'=4 ,试求此时AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O在直线MN上,过点O作射线OP,使∠MOP=130°,现将一块直角三角板的直角顶点始终放在点O处.

(1)如图①,当三角板的一边OA在射线OM上,另一边OB在直线MN的上方时,∠POB的度数 是 ;
(2)若将三角板绕点O旋转至图②所示的位置,此时OB恰好平分∠PON,则∠BOP 的度数为 ;∠AOM 的度数为 ;
(3)若将三角板绕点O旋转至图③所示位置,此时OA在∠PON 的内部,
①若 OP 所在的直线平分∠MOB,则∠POA 的度数为 ;
②∠BON-∠POA的度数为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com