
����Ŀ����ͼ���ھ���ABCD�У�AB��8��BC��6����P����E�ֱ��DZ�AB��BC�ϵĶ��㣬����DP��PE������ADP����BPE�ֱ���DP��PE�۵�����A���B�ֱ����ڵ�A����B������
(1) ����P�˶�����AB���е㴦ʱ����A�����B���غ��ڵ�F��������C��CK��EF��K����CK�ij���
(2) ����P�˶���ijһʱ�̣���P��A'��B'����ǡ����ͬһֱ���ϣ���A'B'��4 �������ʱAP�ij���
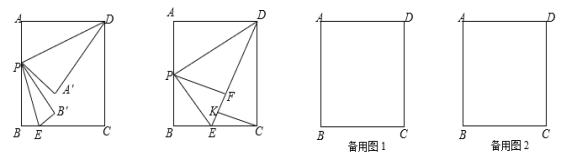
���𰸡���1��![]() ����2��,PA�ij�Ϊ2��6��
����2��,PA�ij�Ϊ2��6��
��������
��1�����۵������ʿɵ�E ,F,D������ͬһֱ���ϣ���Rt��DEC��,���ݹ��ɶ��������BE��CE��DE�ij����ٸ���������������CK��ֵ��
��2������������������ۣ�����A��B����4�г�������⼴��.
����ͼ��
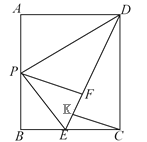
���ı���ABCDΪ���Σ�����ADP����BPE�ֱ���DP��PE�۵���
���PFD����PFE��90��,
���PFD����PFE��180��,����E ,F,D������ͬһֱ���ϣ�
��BE��EF��x,��EC��6��x,
��DC��AB��8, DF��AD��6,
��Rt��DEC��,��DE��DF��FE��6��x, EC��6��x, DC��8,
��(6��x)2��(6��x)2��82,
����ó�x=![]() ,��BE��EF��
,��BE��EF��![]() ,
,
��DE��![]() , EC��
, EC��![]() ,
,
��S��DCE��![]() DCCE��
DCCE��![]() DECK,
DECK,
��CK��![]() ��
��
�Ƣ���ͼ2��,��AP��x,��PB��8��x,
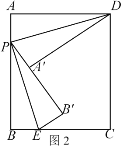
���۵���֪��PA����PA��x , PB����PB��8��x,
��A��B����4,
��8��x��x��4,
��x��2, ��AP��2��
����ͼ3��,
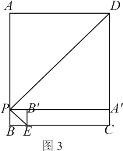
��A��B����4,
��x��(8��x)��4, ��x��6, ��AP��6��
��������,PA�ij�Ϊ2��6��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�E��BC���е㣬����AE���ӳ���DC���ӳ����ڵ�F��

��1����֤��AB=CF��
��2������DE����AD=2AB����֤��DE��AF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����AT�Ǿ�����A�����ߣ���CD��ֱAB��P�㣬QΪ�߶�CP���е㣬����BQ���ӳ�������AT��T�㣬����OT��
��1����֤��BC��OT��
��2������Oֱ��Ϊ10��CD��8����AT�ij���
��3���ӳ�TO��ֱ��CD��R������Oֱ��Ϊ10��CD��8����TR�ij���
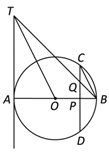
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���û�������ͼ��ʾ�ķ�ʽ��ͼ�Σ����������Ĺ��ɼ�������ȥ�����100��ͼ����Ҫ����________����
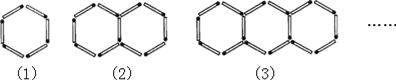
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�P��CD����һ�㣬��AP��BP�ֱ�ƽ�֡�DAB�͡�CBA����AD=5��AP=8�����APB���ܳ��� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����A��B��O�������϶�Ӧ����Ϊa��b��0��������|a+8|+��b��12��2��0����M��N�ֱ��O��B������ͬʱ���������˶���M���ٶ�Ϊ1����λ����ÿ�룬N���ٶ�Ϊ3����λ����ÿ�룬A��B֮��ľ��붨��Ϊ��AB��|a��b|��
��1��ֱ��д��OA���� ����OB���� ����
��2�����˶���ʱ��Ϊt�룬��tΪ��ֵʱ��ǡ����AN��2AM��
��3������PΪ�߶�AM���е㣬QΪ�߶�BN���е㣬M��N���˶��Ĺ����У�PQ+MN�ij����Ƿ����仯�������䣬��˵�����ɣ����仯����tΪ��ֵʱ��PQ+MN����Сֵ����Сֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ֱ�Ѵ���ָ���Բ��ת��A��B�ֳ�4�ȷݡ�3�ȷݵ�����������ÿһ��С�����ڱ�������(��ͼ��ʾ)��������������������ת����Ϸ����Ϸ�����ǣ�ͬʱת������ת�̣���ת��ֹͣʱ����ָ����ָ�����������֮��Ϊ��������ʤ����ָ����ָ�����������֮��Ϊż����������ʤ������ָ�����ڷָ����ϣ�����Ч��������ת��ת�̣�
(1)�����б�����״ͼ�ķ���������ʤ�ĸ��ʣ�
(2)���������Ϸ����Ի���������˫����ƽ����˵�����ɡ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com