
【题目】解方程
(1)2(3x+4)-5(x+1)=4
(2)6-3(x+![]() )=
)=![]()
(3)![]()
(4)![]()
【答案】(1)x=1;(2)x=![]() ;(3)x=
;(3)x=![]() ;(4)x=-
;(4)x=- ![]()
【解析】
(1)方程去括号,移项合并,将x系数化为1,即可求出解;
(2)方程去括号分母,移项合并,将x系数化为1,即可求出解;
(3)方程去分母,去括号,移项合并,将x系数化为1,即可求出解;
(4)方程去分母,去括号,移项合并,将x系数化为1,即可求出解.
(1)2(3x+4)-5(x+1)=4
6x+8-5x-5=4
6x-5x=4+5-8
x=1;
(2)6-3(x+![]() )=
)=![]()
18-9(x+![]() )=2
)=2
18-9x-6=2
-9x=-10
x=![]() ;
;
(3)![]()
4(2x-1)-3(x+2)=12
8x-4-3x-6=12
8x-3x=12+4+6
5x=22
x=![]() ;
;
(4)![]()
6(x+15)=15-10(x-7)
6x+90=15-10x+70
6x+10x=70+15-90
16x=-5
x=-![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点E,点F为对角线BD的三等分点,过点E,点F与BD垂直的直线分别交AB,BC,AD,DC于点M,N,P,Q,MF与PE交于点R,NF与EQ交于点S,已知四边形RESF的面积为5cm2,则菱形ABCD的面积是( )
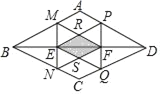
A. 35cm2B. 40cm2C. 45cm2D. 50cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
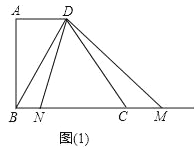
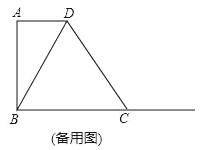
【题目】已知,在梯形ABCD中,AD∥BC,∠A=90°,AD=2,AB=4,BC=5,在射线BC任取一点M,联结DM,作∠MDN=∠BDC,∠MDN的另一边DN交直线BC于点N(点N在点M的左侧).
(1)当BM的长为10时,求证:BD⊥DM;
(2)如图(1),当点N在线段BC上时,设BN=x,BM=y,求y关于x的函数关系式,并写出它的定义域;
(3)如果△DMN是等腰三角形,求BN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形OABC顶点B的坐标为(8,3),定点D的坐标为(12,0),动点P从点O出发,以每秒2个单位长度的速度沿x轴的正方向匀速运动,动点Q从点D出发,以每秒1个单位长度的速度沿x轴的负方向匀速运动,PQ两点同时运动,相遇时停止.在运动过程中,以PQ为斜边在x轴上方作等腰直角三角形PQR.设运动时间为t秒.
(1)当t= 时,△PQR的边QR经过点B;
(2)设△PQR和矩形OABC重叠部分的面积为S,求S关于t的函数关系式;
(3)如图2,过定点E(5,0)作EF⊥BC,垂足为F,当△PQR的顶点R落在矩形OABC的内部时,过点R作x轴、y轴的平行线,分别交EF、BC于点M、N,若∠MAN=45°,求t的值.
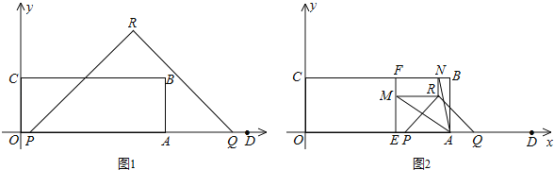
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)
某校为了解“阳光体育”活动的开展情况,从全校![]() 名学生中,随机抽取部分学生进行问卷调查(每名学生只能填写一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.
名学生中,随机抽取部分学生进行问卷调查(每名学生只能填写一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.
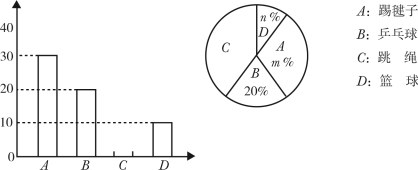
根据以上信息,解答下列问题:
(1)被调查的学生共有 人,并补全条形统计图;
(2)在扇形统计图中,![]() = ,
= ,![]() = ,表示区域
= ,表示区域![]() 的圆心角为 °;
的圆心角为 °;
(3)全校学生中喜欢篮球的人数大约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=6,点P、点E分别是边AB、BC上的动点,连结DP、PE.将△ADP与△BPE分别沿DP与PE折叠,点A与点B分别落在点A′,B′处.
(1) 当点P运动到边AB的中点处时,点A′与点B′重合于点F处,过点C作CK⊥EF于K,求CK的长;
(2) 当点P运动到某一时刻,若P,A',B'三点恰好在同一直线上,且A'B'=4 ,试求此时AP的长.
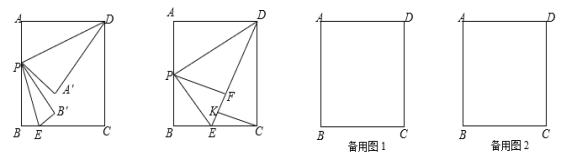
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在日历中任意圈出一个3×3的正方形,则里面九个数不满足的关系式是( )

A. a1+a2+a3+a7+a8+a9=2(a4+a5+a6)
B. a1+a4+a7+a3+a6+a9=2(a2+a5+a8)
C. a1+a2+a3+a4+a5+a6+a7+a8+a9=9a5
D. (a3+a6+a9)﹣(a1+a4+a7)=(a2+a5+a8)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】无锡阳山水蜜桃上市后,甲、乙两超市分别用60000元以相同的进价购进相同箱数的水蜜桃,甲超市销售方案是:将水蜜桃按分类包装销售,其中挑出优质大个的水蜜桃400箱,以进价的2倍价格销售,剩下的水蜜桃以高于进价10%销售.乙超市的销售方案是:不将水蜜桃分类,直接销售,价格按甲超市分类销售的两种水蜜桃售价的平均数定价.若两超市将水蜜桃全部售完,其中甲超市获利42000元(其它成本不计).问:
(1)水蜜桃进价为每箱多少元?
(2)乙超市获利多少元?哪种销售方式更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把2016个正数1、2、3、4…,2016按如图的方式排列成一个表.
(1)如图,用一个正方形框在表中任意框住4个数,记左上角的一个数为x,则另外三个数用含x的式子从小到大依次表示为 , , .
(2)当被框住的4个数的和等于416时,x的值为多少?
(3)能否框住4个数,使它们的和等于324?如能,求出x的值;如不能,请说出理由.
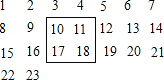
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com