
【题目】如图,在△ABC中,CD⊥AB于点D,AE⊥BC于点E,AE、CD交于点F,且∠DBF=45°.
(1)若AF=![]() ,BF=
,BF=![]() ,求AB的长;
,求AB的长;
(2)求证:AB﹣CF=![]() BF.
BF.

【答案】(1)AB=3;(2)见解析.
【解析】
(1)由等腰直角三角形的性质和勾股定理可求DF=BD=1,由勾股定理可求AD=2,即可求AB的长;
(2)由“AAS”可证△ADF≌△BCD,可得AD=CD,即可证等式成立.
(1)∵∠DBF=45°,CD⊥AB,
∴∠DFB=∠DBF=45°,
∵DF2+DB2=BF2,且BF=![]()
∴DF=BD=1,
在Rt△ADF中,AD=![]() =2,
=2,
∴AB=AD+DB=2+1=3;
(2))∵∠DBF=45°,CD⊥AB,
∴∠DFB=∠DBF=45°,
∴DF=DB,
∴BF=![]() DF,
DF,
∵AE⊥BC,CD⊥AB,
∴∠ABC+∠EAB=90°,∠ABC+∠DCB=90°,
∴∠EAB=∠DCB,且DF=DB,∠ADF=∠CDB=90°,
∴△ADF≌△BCD(AAS),
∴AD=CD,
∵AB﹣CF=AD+DB﹣CF=DF+BD=2DF=![]() BF
BF


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】某工厂准备购买A、B两种零件,已知A种零件的单价比B种零件的单价多30元,而用900元购买A种零件的数量和用600元购买B种零件的数量相等.
(1)求A、B两种零件的单价;
(2)根据需要,工厂准备购买A、B两种零件共200件,工厂购买两种零件的总费用不超过14700元,求工厂最多购买A种零件多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
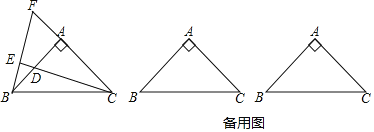
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F.
(1)点D在边AB上时,证明:AB=FA+BD;
(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请画出图形并直接写出正确结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=∠COD,若∠AOD=110°,∠BOC=70°,则以下结论正确的有( )

①∠AOC=∠BOD=90°;②∠AOB=20°;③∠AOB=∠AOD-∠AOC;④∠AOB=![]() ∠BOD.
∠BOD.
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若BC=EC,∠BCE=∠ACD,则添加不能使△ABC≌△DBC的条件是( )
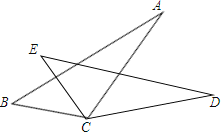
A.AB=DE B.∠B=∠E C.AC=DC D.∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】榴莲是热带著名水果之一,榴莲营养极为丰富,含有蛋白质、糖类、多种维生素、膳食纤维、脂肪、叶酸,氨基酸和矿物质,有强身健体、滋阴补阳之功效.它的气味浓烈、爱之者赞其香,厌之者怨其臭,喜欢榴莲的人也喜欢榴莲干,榴莲千层,榴莲披萨、榴莲酥等榴莲加工制品,某校数学兴趣小组为了了解本校学生喜爱榴莲的情况,随机抽取了200名学进行问卷调查,经过统计后绘制了两幅尚不完整的统计图.(注:每一位同学在任何一种分类统计中只有一种选择)

请根据统计图完成下列问题:
(1)扇形统计图中,“很喜欢”所对应的圆心角度数为______度;喜欢榴莲千层的人数为______人;请补全条形统计图.
(2)若该校学生人数为8000人,请根据上述调查结果,估计该校学生中最爱吃榴莲干和榴莲酥的人数之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,⊿ABC的顶点在格点上。 且A(1,-4),B(5,-4),C(4,-1)
【1】画出⊿ABC;
【1】求出⊿ABC 的面积;![]()
【1】若把⊿ABC向上平移2个单位长度,再向左平移4个单位长度得到⊿![]()
![]() B
B![]() C
C![]() ,在图中画出⊿
,在图中画出⊿![]()
![]() B
B![]() C
C![]() ,并写出B
,并写出B![]() 的坐标。
的坐标。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com