Question

【题目】如图，△ABC中，AB=AC，∠BAC=90°，点D是直线AB上的一动点（不和A、B重合），BE⊥CD于E，交直线AC于F．

(1)点D在边AB上时，证明：AB=FA+BD；

(2)点D在AB的延长线或反向延长线上时，(1)中的结论是否成立？若不成立，请画出图形并直接写出正确结论．

Answer 1

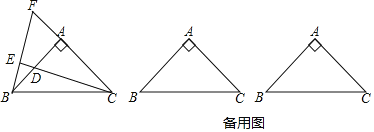
【答案】(1)证明见解析；(2)见解析.

【解析】

（1）易证∠FBA=∠FCE，结合条件容易证到△FAB≌△DAC，从而有FA=DA，就可得到AB=AD+BD=FA+BD．
（2）由于点D的位置在变化，因此线段AF、BD、AB之间的大小关系也会相应地发生变化，只需画出图象并借鉴（1）中的证明思路就可解决问题．

(1)如图1，∵BE⊥CD，即∠BEC=90°，∠BAC=90°，

∴∠F+∠FBA=90°，∠F+∠FCE=90°．

∴∠FBA=∠FCE．

∵∠FAB=180°-∠DAC=90°，

∴∠FAB=∠DAC．

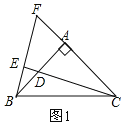
∵AB=AC，

∴△FAB≌△DAC．

∴FA=DA．

∴AB=AD+BD=FA+BD．

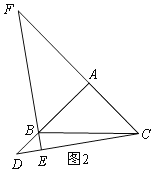
(2)如图2，当D在AB延长线上时，AF=AB+BD，

理由是：同理得：△FAB≌△DAC，

∴AF=AD=AB+BD；

如图3，当D在AB反向延长线上时，BD=AB+AF，

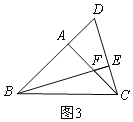
理由是：同理得：△FAB≌△DAC，

∴AF=AD，

∴BD=AB+AD=AB+AF．