
【题目】已知:如图,△ABC是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间t(s),解答下列各问题: 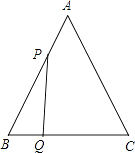
(1)经过 ![]() 秒时,求△PBQ的面积;
秒时,求△PBQ的面积;
(2)当t为何值时,△PBQ是直角三角形?
(3)是否存在某一时刻t,使四边形APQC的面积是△ABC面积的三分之二?如果存在,求出t的值;不存在请说明理由.
【答案】
(1)解:经过 ![]() 秒时,AP=
秒时,AP= ![]() cm,BQ=
cm,BQ= ![]() cm,
cm,
∵△ABC是边长为3cm的等边三角形,
∴AB=BC=3cm,∠B=60°,
∴BP=3﹣ ![]() =
= ![]() cm,
cm,
∴△PBQ的面积= ![]() BPBQsin∠B=
BPBQsin∠B= ![]() ×
× ![]() ×
× ![]() ×
× ![]() =
= ![]()
(2)解:设经过t秒△PBQ是直角三角形,
则AP=tcm,BQ=tcm,
△ABC中,AB=BC=3cm,∠B=60°,
∴BP=(3﹣t)cm,
△PBQ中,BP=(3﹣t)cm,BQ=tcm,若△PBQ是直角三角形,则∠BQP=90°或∠BPQ=90°,
当∠BQP=90°时,BQ= ![]() BP,
BP,
即t= ![]() (3﹣t),t=1(秒),
(3﹣t),t=1(秒),
当∠BPQ=90°时,BP= ![]() BQ,
BQ,
3﹣t= ![]() t,t=2(秒),
t,t=2(秒),
答:当t=1秒或t=2秒时,△PBQ是直角三角形
(3)解:过P作PM⊥BC于M,
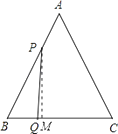
△BPM中,sin∠B= ![]() ,
,
∴PM=PBsin∠B= ![]() (3﹣t),
(3﹣t),
∴S△PBQ= ![]() BQPM=
BQPM= ![]() t
t ![]() (3﹣t),
(3﹣t),
∴y=S△ABC﹣S△PBQ= ![]() ×32×
×32× ![]() ﹣
﹣ ![]() ×t×
×t× ![]() (3﹣t)
(3﹣t)
= ![]() t2﹣
t2﹣ ![]() t+
t+ ![]() ,
,
∴y与t的关系式为y= ![]() t2﹣
t2﹣ ![]() t+
t+ ![]() ,
,
假设存在某一时刻t,使得四边形APQC的面积是△ABC面积的 ![]() ,
,
则S四边形APQC= ![]() S△ABC,
S△ABC,
∴ ![]() t2﹣
t2﹣ ![]() t+
t+ ![]() =
= ![]() ×
× ![]() ×32×
×32× ![]() ,
,
∴t2﹣3t+3=0,
∵(﹣3)2﹣4×1×3<0,
∴方程无解,
∴无论t取何值,四边形APQC的面积都不可能是△ABC面积的 ![]() .
.
【解析】(1)根据路程=速度×时间,求出BQ,AP的值,再求出BP的值,然后利用三角形的面积公式进行解答即可;(2)①∠BPQ=90°;②∠BQP=90°.然后在直角三角形BQP中根据BP,BQ的表达式和∠B的度数进行求解即可.(3)本题可先用△ABC的面积﹣△PBQ的面积表示出四边形APQC的面积,即可得出y,t的函数关系式,然后另y等于三角形ABC面积的三分之二,可得出一个关于t的方程,如果方程无解则说明不存在这样的t值,如果方程有解,那么求出的t值即可


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与y轴交于点A(0,-
与y轴交于点A(0,- ![]() ),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.
),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.

(1)求AB所在直线的函数表达式;
(2)请你判断△ABD的形状并证明你的结论;
(3)点E在线段AD上运动且与点A、D不重合,点F在直线l上运动,且∠BEF=60°,连接BF,求出△BEF面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“囧”(jiǒng).经是一个风靡网络的流行词,像一个人脸郁闷的神情.如图所示,一张边长为20cm的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为xcm、ycm.剪去的两个小直角三角形的两宜角边长也分别为xcm,ycm. 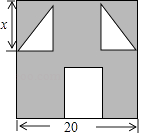
(1)用含有x,y的代数式表示图中“囧”(阴影部分)的面积;
(2)当x=8cm,y=6cm时,求此时“囧”(阴影部分)的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店有两种进价不同的计算机都卖了64元,其中一个赢利60%,另一个亏本20%,在这次买卖中这家商店( )
A. 不赔不赚 B. 赚了8元 C. 赔了8元 D. 赚了32元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com