
【题目】如图,抛物线![]() 与y轴交于点A(0,-
与y轴交于点A(0,- ![]() ),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.
),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.

(1)求AB所在直线的函数表达式;
(2)请你判断△ABD的形状并证明你的结论;
(3)点E在线段AD上运动且与点A、D不重合,点F在直线l上运动,且∠BEF=60°,连接BF,求出△BEF面积的最小值.
【答案】(1)![]() (2)△ABD是等边三角形,(3)
(2)△ABD是等边三角形,(3)![]()
【解析】试题分析:(1)先求得抛物线的解析式,再求得点B、C的坐标,再由待定系数法求出直线AB的解析式;(2)△ABD是等边三角形,根据已知条件易证△BOA≌△DOA,可得BA=DA,根据锐角三角函数可求得∠ABO=60°,即可判定△ABD是等边三角形;(3)过点E作EG∥x轴,交AB于点G, 易证△AEG是等边三角形,可得AE=AG,再证△BEG≌△EFD,可得BE=EF,易得△BEF是等边三角形 ,当BE⊥AD时,BE的长度最小,则△BEF的面积取最小值,求得△BEF面积的最小值即可.
试题解析:
(1)将点A(0,- ![]() )代入抛物线解析式中,得c=-
)代入抛物线解析式中,得c=-![]() ,
,
![]()
![]()
当y=0时, ![]()
化简得x2-2x-3=0
![]() (x+1)(x-3)=0
(x+1)(x-3)=0
![]() x 1=-1, x 2=3
x 1=-1, x 2=3
![]() 点B (-1,0),点C(3,0)
点B (-1,0),点C(3,0)
设直线AB的表达式为y=kx+b,
![]() 图象经过点A(0,-
图象经过点A(0,- ![]() ),点B (-1,0),
),点B (-1,0),
代入得 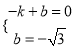 ,解得
,解得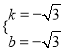
![]() 直线AB的表达式为
直线AB的表达式为![]()
(2)△ABD是等边三角形,
![]() 点B(-1,0), 点D(1,0)
点B(-1,0), 点D(1,0)
![]() OB=OD=1,
OB=OD=1,
∵OA是公共边,∠BOA=∠DOA=90°,
∴△BOA≌△DOA,
∴BA=DA,
tan∠ABO=![]() ,
,
∴∠ABO=60°,
![]() △ABD是等边三角形
△ABD是等边三角形
(3)过点E作EG∥x轴,交AB于点G,
∵△ABD是等边三角形
∴∠BAD=∠ABD=∠ADB=60°
∴∠AEG=∠AGE=60°
∴△AEG是等边三角形,
∴AE=AG
∴DE=BG
∵AB∥l
∴∠
∴∠GBE+∠GEB=60°,∠DEF+∠GEB=60°,
∴∠GBE=∠DEF
∴△BEG≌△EFD
∴BE=EF
又∵∠BEF=60°
∴△BEF是等边三角形
∴S△BEF=![]()
当BE⊥AD时,BE的长度最小,则△BEF的面积取最小值,
此时,BE=ABsin60°=![]() ,
,
△BEF面积的最小值=![]() =
=![]()



科目:初中数学 来源: 题型:
【题目】综合题。
(1)根据图示规律填表: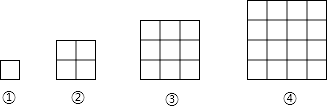
图形编号 | 1×1的正方形个数 | 2×2的正方形个数 | 3×3的正方形个数 | 4×4的正方形个数 |
① | ||||
② | ||||
③ | ||||
④ |
(2)猜想:第n个图形共有多少个正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在植树节到来之际,某小区计划购进A、B两种树苗共17棵,已知A种树苗每棵80元,B种树苗每棵60元.
(1)若购进A、B两种树苗刚好用去1220元,问购进A、B两种树苗各多少棵?
(2)若购买B种树苗的数量少于A种树苗的数量,请你给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画三视图时,首先确定主视图的位置.画出主视图,然后在主视图的下面画出俯视图,在主视图的右面画出左视图.主视图反映物体的_______和_______,俯视图反映物体的_______和_______,左视图反映物体的_______和_______.因此,画三视图时,主、俯视图要长对正,主、左视图要高平齐,左、俯视图要宽相等.看得见部分的轮廓线通常画成实线,看不见部分的轮廓线通常画成虚线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.请根据图中的数据(单位:m),解答下列问题: 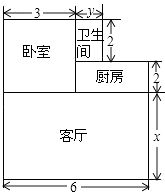
(1)用含x、y的代数式表示地面总面积;
(2)若x=5,y= ![]() ,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?
,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间t(s),解答下列各问题: 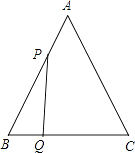
(1)经过 ![]() 秒时,求△PBQ的面积;
秒时,求△PBQ的面积;
(2)当t为何值时,△PBQ是直角三角形?
(3)是否存在某一时刻t,使四边形APQC的面积是△ABC面积的三分之二?如果存在,求出t的值;不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知蜗牛从A点出发,在一条数轴上来回爬行,规定:向正半轴运动记作“+”,向负半轴运动记作“﹣”,从开始到结束爬行的各段路程(单位:cm)依次为:+7,﹣5,﹣10,﹣8,+9,﹣6,+12,+4
(1)若A点在数轴上表示的数为﹣3,则蜗牛停在数轴上何处,请通过计算加以说明;
(2)若蜗牛的爬行速度为每秒 ![]() ,请问蜗牛一共爬行了多少秒?
,请问蜗牛一共爬行了多少秒?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com