
【题目】如图1,已知矩形ABED(两组对边分别相等,四个内角都是直角),点C是边DE的中点,且AB=2AD.
(1)判断△ABC的形状,并说明理由;
(2)保持图1中△ABC固定不变,绕点C旋转DE所在的直线MN到图2中(当垂线段AD、BE在直线MN的同侧),试探究线段AD、BE、DE长度之间有什么关系?并给予证明;
(3)保持图2中△ABC固定不变,继续绕点C旋转DE所在的直线MN到图3中的位置(当垂线段AD、BE在直线MN的异侧).试探究线段AD、BE、DE长度之间有什么关系?并给予证明.
 2
2
【答案】(1)△ABC是等腰直角三角形.理由见解析;
(2)DE=AD+BE.理由见解析;
(3)DE=BE-AD.理由见解析.
【解析】试题分析:(1)根据矩形的性质及勾股定理,即可判断△ABC的形状;
(2)先证明△ACD≌△CBE,然后根据线段之间的关系可得AD、BE、DE长度之间的关系;(3)通过证明△ACD≌△CBE,根据全等三角形的性质得出即可得线段AD、BE、DE长度之间的关系.
试题解析:(1)△ABC是等腰直角三角形.理由如下:
在△ADC与△BEC中,AD=BE,∠D=∠E=90°,DC=EC,
∴△ADC≌△BEC(SAS),
∴AC=BC,∠DCA=∠ECB.
∵AB=2AD=DE,DC=CE,
∴AD=DC,
∴∠DCA=45°,
∴∠ECB=45°,
∴∠ACB=180°-∠DCA-∠ECB=90°.
∴△ABC是等腰直角三角形.
(2)DE=AD+BE.理由如下:
在△ACD与△CBE中,∠ACD=∠CBE=90°-∠BCE,∠ADC=∠BEC=90°,AC=BC,
∴△ACD≌△CBE(AAS),
∴AD=CE,DC=EB.
∴DC-CE=BE-AD,
即DE=AD+BE.
(3)DE=BE-AD.理由如下:
在△ACD与△CBE中,∠ACD=∠CBE=90°-∠BCE,∠ADC=∠BEC=90°,AC=BC,
∴△ACD≌△CBE(AAS),
∴AD=CE,DC=EB.
∴DC-CE=BE-AD,
即DE=BE-AD.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
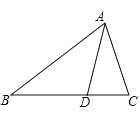
【题目】如图,D是△ABC的BC边上的一点,AD=BD,∠ADC=80°.
(1)求∠B的度数;
(2)若∠BAC=70°,判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题7分)数学课上,探讨角平分线的作法时,李老师用直尺和圆规作角平分线,方法如下:
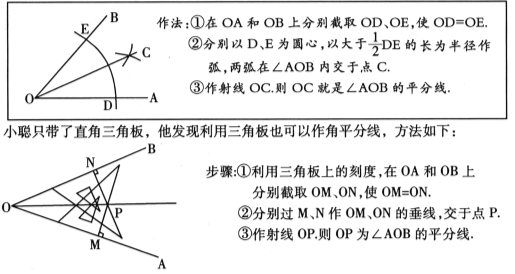
根据以上情境,解决下列问题:
(1)李老师用尺规作角平分线时,用到的三角形全等的判定方法是 .
(2)小聪的作法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2;乙袋中的小球上分别标有数字﹣1,﹣2,0.现从甲袋中任意摸出一个小球,记其标有的数字为x,再从乙袋中任意摸出一个小球,记其标有的数字为y,以此确定点M的坐标(x,y).
(1)请你用画树状图或列表的方法,写出点M所有可能的坐标;
(2)求点M(x,y)在函数![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果将抛物线y=(x﹣2)2+1向左平移1个单位,再向上平移3个单位,那么所得新抛物线的解析式为( )
A.y=(x﹣3)2+4B.y=(x﹣1)2+4C.y=(x+1)2+2D.y=(x+1)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com