练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

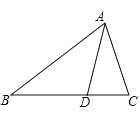
    【题目】如图，D是△ABC的BC边上的一点，AD=BD，∠ADC=80°．

    （1）求∠B的度数；

    （2）若∠BAC=70°，判断△ABC的形状，并说明理由．

    【答案】（1）40°；（2）△ABC是等腰三角形．证明见解析.

    【解析】试题分析：（1）由由三角形外角的性质，可求得∠BAD的度数，根据等角对等边，可得AD=BD；

    （2）由∠BAC=70°，易求得∠C=∠BAC=70°，根据等角对等边的性质，可证得△ABC是等腰三角形．

    （1）∵∠ADC=∠B+∠BAD，而∠ADC=80°，∠B =40°，

    ∴∠BAD=80°-40°=40°，

    ∴∠B=∠BAD，

    ∴AD=BD.

    （2）△ABC是等腰三角形．

    理由：∵∠B=40°，∠BAC=70°，

    ∴∠C=180°﹣∠B﹣∠BAC=70°，

    ∴∠C=∠BAC，

    ∴BA=BC，

    ∴△ABC是等腰三角形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

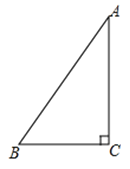
    【题目】如图，在Rt△ABC中，∠ACB=90°．

    （1）请用直尺和圆规按下列步骤作图，保留作图痕迹：

    ①作∠ACB的平分线，交斜边AB于点D；

    ②过点D作AC的垂线，垂足为点E．

    (2)在（1）作出的图形中，若CB=6，DE=4，则△BCD的面积为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】关于以下说法：①买一张彩票一定中奖；②从一副普通扑克牌中任意抽取一张，一定是红桃；判断正确的是（ ）

    A.①②都正确B.只有①正确C.只有②正确D.①②都错误

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，直线l过正方形ABCD的顶点B，点A、C到直线l的距离分别是AE=1，CF=2，则EF长为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列命题，其中是真命题的为（ ）

    A.一组对边平行，另一组对边相等的四边形是平行四边形

    B.一组邻边相等的矩形是正方形

    C.对角线相等的四边形是矩形

    D.对角线互相垂直的四边形是菱形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，点O为坐标原点，直线l与抛物线相交于A（1，），B（4，0）两点．

    （1）求出抛物线的解析式；

    （2）在坐标轴上是否存在点D，使得△ABD是以线段AB为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；

    （3）点P是线段AB上一动点，（点P不与点A、B重合），过点P作PM∥OA，交第一象限内的抛物线于点M，过点M作MC⊥x轴于点C，交AB于点N，若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN，求出的值，并求出此时点M的坐标．

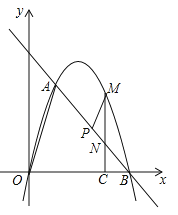
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，点P（2，3）关于x轴的对称点坐标为（ ）
    A.（﹣2，3）
    B.（2，﹣3）
    C.（3，﹣2）
    D.（﹣2，﹣3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】四边形ABCD中，∠A=∠C=90°，BE、DF分别是∠ABC、∠ADC的平分线．求证：

    （1）∠1+∠2=90°；

    （2）BE∥DF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知矩形ABED（两组对边分别相等，四个内角都是直角），点C是边DE的中点，且AB=2AD．

    （1）判断△ABC的形状，并说明理由；

    （2）保持图1中△ABC固定不变，绕点C旋转DE所在的直线MN到图2中（当垂线段AD、BE在直线MN的同侧），试探究线段AD、BE、DE长度之间有什么关系？并给予证明；

    （3）保持图2中△ABC固定不变，继续绕点C旋转DE所在的直线MN到图3中的位置（当垂线段AD、BE在直线MN的异侧）．试探究线段AD、BE、DE长度之间有什么关系？并给予证明．

    2

    查看答案和解析>>

    同步练习册答案