
【题目】已知关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根x1,x2,请用配方法探索有实数根的条件,并推导出求根公式,证明x1x2=![]() .
.
科目:初中数学 来源: 题型:
【题目】小方家住户型呈长方形,平面图如下(单位:米),现准备铺设地面,三间卧室铺设木地板,其它区城铺设地砖.
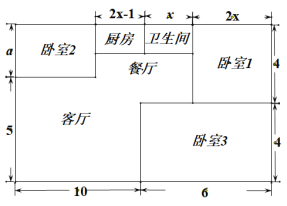
(1)求a的值.
(2)铺设地面需要木地板和地砖各多少平方米(用含![]() 的代数式表示)?
的代数式表示)?
(3)按市场价格,木地板单价为300元/平方米,地砖单价为100元/平方米,装修公司有![]() 两种活动方案,如表:
两种活动方案,如表:
活动方案 | 木地板价格 | 地砖价格 | 总安装费 |
A | 8折 | 8.5折 | 2000元 |
B | 9折 | 8.5折 | 免收 |
已知卧室2的面积是21平方米,则小方家应选择哪种活动,使铺设地面的总费用(包括材料费及安装费)更低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现:如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,则∠AEB的度数为 ,线段AD、BE之间的关系 .
(2)拓展探究:如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.①请判断∠AEB的度数,并说明理由;②当CM=5时,AC比BE的长度多6时,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地试行医保制度,并规定:
一、每位居民年初缴纳医保基金70元;
二、居民个人当年看病的医疗费(以定点医院的医疗发票为准,年底按下表所示的方式结算)报销看病的医疗费用.
居民个人当年看病的医疗费用 | 医疗费用报销办法 |
不超过 n 元的部分 | 全部由医保基金承担(即全额报销) |
超过 n 元但不超过 6 000 元的部分 | 个人承担 |
超过 6 000 元的部分 | 个人承担 |
设一位居民当年看病的医疗费用为![]() 元,他个人实际承担的医疗费用(包括医疗费用中个人承担的部分和年初缴纳的医保基金)记为
元,他个人实际承担的医疗费用(包括医疗费用中个人承担的部分和年初缴纳的医保基金)记为![]() 元.
元.
(1)写出如下条件,![]() 的代数式(可含有
的代数式(可含有![]() ).
).
①当![]() 时;
时;
②当![]() 时.
时.
(2)已知![]() ,若该地居民周大爷某一年个人实际承担的医疗费用是
,若该地居民周大爷某一年个人实际承担的医疗费用是![]() 元,那么他这一年看病所花费的医疗费共多少元?
元,那么他这一年看病所花费的医疗费共多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个边长为![]() 的大正方形,剪去一个边长为
的大正方形,剪去一个边长为![]() 的小正方形后,得到图①,称之为“前世”,然后再剪拼成一个新长方形即图②,称之为“今生”,请你解答下面的问题:
的小正方形后,得到图①,称之为“前世”,然后再剪拼成一个新长方形即图②,称之为“今生”,请你解答下面的问题:
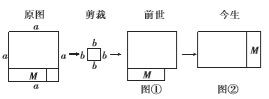
(1)“前世”图①的面积与“今生”图②新长方形的面积______;
(2)根据图形面积的和差关系直接写出“前世”图①的面积为_______,标明“今生”图②新长方形的长为______、宽为_______、面积为_______;
(3)“形缺数时少直观,数缺形时少形象”它体现了数学的数形结合思想,由(1)和(2)图形面积的计算,形象地验证了代数中的一个乘法公式:______;
(4)利用本题所得公式计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程x2+(2k+1)x+k2+2=0有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)若x1,x2满足|x1|+|x2|=|x1x2|-1,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D.
(1)如图1,点E,F在AB,AC上,且∠EDF=90°.求证:BE=AF;
(2)点M,N分别在直线AD,AC上,且∠BMN=90°.
①如图2,当点M在AD的延长线上时,求证:AB+AN=![]() AM;
AM;
②当点M在点A,D之间,且∠AMN=30°时,已知AB=2,直接写出线段AM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车经销商计划投入7.1万元购进100辆A型和30辆B型自行车,其中B型车单价是A型车单价的6倍少60元.
(1)求A、B两种型号的自行车单价分别是多少元?
(2)后来由于该经销商资金紧张,投入购车的资金不超过5.86万元,但购进这批自行年的总数不变,那么至多能购进B型车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
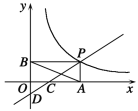
【题目】如图,直线![]() 与x轴、y轴分别交于C、D两点,与双曲线
与x轴、y轴分别交于C、D两点,与双曲线![]() 在第一象限内交于点P,过点P作PA⊥x轴于点A,PB⊥y轴于点B,已知B(0,4)且S△DBP=27.
在第一象限内交于点P,过点P作PA⊥x轴于点A,PB⊥y轴于点B,已知B(0,4)且S△DBP=27.
(1)直接写出直线的解析式_____________,双曲线的解析式____________;
(2)设点Q是直线![]() 上的一点,且满足△DOQ的面积是△COD面积的2倍,请求出点Q的坐标;
上的一点,且满足△DOQ的面积是△COD面积的2倍,请求出点Q的坐标;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com