
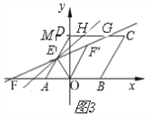
°æƒø°ø‘Ğ∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨O «◊¯±Í‘≠µ„£¨ABCDµƒ∂•µ„Aµƒ◊¯±ÍŒ™£®©Å2£¨0£©£¨µ„Dµƒ◊¯±ÍŒ™£®0£¨2![]() £©£¨µ„B‘Ğx÷·µƒ’˝∞Î÷·…œ£¨µ„EŒ™œş∂ŒADµƒ÷–µ„£Æ
£©£¨µ„B‘Ğx÷·µƒ’˝∞Î÷·…œ£¨µ„EŒ™œş∂ŒADµƒ÷–µ„£Æ
£®¢Ò£©»ÁÕº1£¨«Û°œDAOµƒ¥Û–°º∞œş∂ŒDEµƒ≥§£ª
£®¢Ú£©π˝µ„Eµƒ÷±œşl”Îx÷·Ωª”е„F£¨”Î…‰œşDCΩª”е„G£Æ¡¨Ω”OE£¨°˜OEF°‰ «°˜OEFπÿ”Ğ÷±œşOE∂‘≥∆µƒÕº–Œ£¨º«÷±œşEF°‰”Î…‰œşDCµƒΩªµ„Œ™H£¨°˜EHCµƒ√ʪ˝Œ™3![]() £Æ
£Æ
¢Ÿ»ÁÕº2£¨µ±µ„G‘е„Hµƒ◊Û≤‡ ±£¨«ÛGH£¨DGµƒ≥§£ª
¢Ğµ±µ„G‘е„Hµƒ”“≤‡ ±£¨«Ûµ„Fµƒ◊¯±Í£®÷±Ω”–¥≥ˆΩ·π˚º¥ø…£©£Æ

°æ¥∞∏°ø£®¢Ò£©30°„£¨2£ª£®¢Ú£©¢Ÿ3+![]() £¨-3+
£¨-3+![]() £ª¢ĞF£®©Å5©Å
£ª¢ĞF£®©Å5©Å![]() £¨0£©£Æ
£¨0£©£Æ
°æΩ‚Œˆ°øΩ‚£∫£®¢Ò£©°şA£®©Å2£¨0£©£¨D£®0£¨2![]() £©°‡AO=2£¨DO=2
£©°‡AO=2£¨DO=2![]() £¨°‡tan°œDAO=
£¨°‡tan°œDAO=![]() =
=![]() £¨
£¨
°‡°œDAO=60°„£¨°‡°œADO=30°„£¨°‡AD=2AO=4£¨°şµ„EŒ™œş∂ŒAD÷–µ„£¨°‡DE=2£ª
£®¢Ú£©¢Ÿ»ÁÕº2£¨

π˝µ„E◊˜EM°ÕCD£¨°‡CD°ŒAB£¨°‡°œEDM=°œDAB=60°„£¨°‡EM=DEsin60°„=![]() £¨°‡GH=6£¨
£¨°‡GH=6£¨
°şCD°ŒAB£¨°‡°œDGE=°œOFE£¨
°ş°˜OEF°‰ «°˜OEFπÿ”Ğ÷±œşOEµƒ∂‘≥∆Õº–Œ£¨°‡°˜OEF°‰°’°˜OEF£¨°‡°œOFE=°œOF°‰E£¨
°şµ„E «ADµƒ÷–µ„£¨°‡OE=![]() AD=AE£¨
AD=AE£¨
°ş°œEAO=60°„£¨°‡°˜EAO «µ»±ş»˝Ω«–Œ£¨°‡°œEOA=60°„£¨°œAEO=60°„£¨
°ş°˜OEF°‰°’°˜OEF£¨°‡°œEOF°‰=°œEOA=60°„£¨
°‡°œEOF°‰=°œAEO£¨°‡AD°ŒOF°‰£¨°‡°œOF°‰E=°œDEH£¨°‡°œDEH=°œDGE£¨
°ş°œDEH=°œEDG£¨°‡°˜DHE°◊°˜DEG£¨°‡![]() £¨°‡DE2=DG°¡DH£¨
£¨°‡DE2=DG°¡DH£¨
…ËDG=x£¨‘ÚDH=x+6£¨°‡4=x£®x+6£©£¨°‡x1=©Å3+![]() £¨x2=©Å3©Å
£¨x2=©Å3©Å![]() £¨°‡DG=©Å3+
£¨°‡DG=©Å3+![]() £Æ
£Æ
¢Ğ»ÁÕº3£¨
π˝µ„E◊˜EM°ÕCD£¨°‡CD°ŒAB£¨°‡°œEDM=°œDAB=60°„£¨°‡EM=DEsin60°„=![]() £¨°‡GH=6£¨
£¨°‡GH=6£¨
°şCD°ŒAB£¨°‡°œDHE=°œOFE£¨
°ş°˜OEF°‰ «°˜OEFπÿ”Ğ÷±œşOEµƒ∂‘≥∆Õº–Œ£¨°‡°˜OEF°‰°’°˜OEF£¨°‡°œOFE=°œOF°‰E£¨
°şµ„E «ADµƒ÷–µ„£¨°‡OE=![]() AD=AE£¨
AD=AE£¨
°ş°œEAO=60°„£¨°‡°˜EAO «µ»±ş»˝Ω«–Œ£¨°‡°œEOA=60°„£¨°œAEO=60°„£¨
°ş°˜OEF°‰°’°˜OEF£¨°‡°œEOF°‰=°œEOA=60°„£¨°‡°œEOF°‰=°œAEO£¨°‡AD°ŒOF°‰£¨
°‡°œOF°‰E=°œDEH£¨°‡°œDEG=°œDHE£¨
°ş°œDEG=°œEDH£¨°‡°˜DGE°◊°˜DEH£¨°‡![]() £¨°‡DE2=DG°¡DH£¨
£¨°‡DE2=DG°¡DH£¨
…ËDH=x£¨‘ÚDG=x+6£¨°‡4=x£®x+6£©£¨°‡x1=©Å3+![]() £¨x2=©Å3©Å
£¨x2=©Å3©Å![]() £¨
£¨
°‡DH=©Å3+![]() £Æ°‡DG=3+
£Æ°‡DG=3+![]() °‡DG=AF=3+
°‡DG=AF=3+![]() £¨°‡OF=5+
£¨°‡OF=5+![]() £¨°‡F£®©Å5©Å
£¨°‡F£®©Å5©Å![]() £¨0£©£Æ
£¨0£©£Æ



| ƒÍº∂ | ∏ş÷–øŒ≥à | ƒÍº∂ | ≥÷–øŒ≥à |
| ∏ş“ª | ∏ş“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥“ª | ≥“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏ş∂˛ | ∏ş∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥∂˛ | ≥∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏ş»˝ | ∏ş»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥»˝ | ≥»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘Ğ∆Ω––Àƒ±ş–ŒABCD÷–£¨E£¨FŒ™∂‘Ω«œşBD…œµƒ¡Ωµ„£¨«“°œDAE£Ω°œBCF£Æ
«Û÷§£∫£®1£©AE£ΩCF£ª
£®2£©Àƒ±ş–ŒAECF «∆Ω––Àƒ±ş–Œ£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™“ª¥Œ∫Ø ˝µƒÕºœÛπ˝M(1,3),N(-2,12)¡Ωµ„.
(1)«Û∫Ø ˝µƒΩ‚Œˆ Ω;
(2) ‘≈–∂œµ„P(2a,-6a+8) «∑Ò‘Ğ∫Ø ˝µƒÕºœÛ…œ,≤¢Àµ√˜¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒø«∞Œ“ –°∞–£‘∞ ÷ª˙°±œ÷œÛ‘Ω¿¥‘Ω İµΩ…Áª·πÿ◊¢£¨’Î∂‘’‚÷÷œ÷œÛ£¨÷ÿ«Ï“ª÷–≥»˝£®1£©∞‡ ˝—ß–À»§–°◊ȵƒÕ¨—ßÀʪ˙µ˜≤È¡À—ß–£»Ù∏…√˚º“≥§∂‘°∞÷–—ß…˙¥¯ ÷ª˙°±œ÷œÛµƒÃ¨∂»£®Ã¨∂»∑÷Œ™£∫A£ÆŒŞÀ˘ŒΩ£ªB£Æª˘±æ‘Ş≥…£ªC£Æ‘Ş≥…£ªD£Æ∑¥∂‘£©£¨≤¢Ω´µ˜≤ÈΩ·π˚ªÊ÷∆≥…∆µ ˝’ğœşÕ≥º∆Õº1∫Õ…»–ŒÕ≥º∆Õº2£®≤ªÕÍ’˚£©£Æ«Î∏˘æıÕº÷–Ã·π©µƒ–≈œ¢£¨Ω‚¥œ¬¡–Œ £∫
£®1£©¥À¥Œ≥È—˘µ˜≤È÷–£¨π≤µ˜≤È¡À∂‡…Ÿ√˚÷–—ß…˙º“≥§£ª
£®2£©«Û≥ˆÕº2÷–…»–ŒCÀ˘∂‘µƒ‘≤–ƒΩ«µƒ∂» ˝£¨≤¢Ω´Õº1≤π≥‰ÕÍ’˚£ª
£®3£©∏˘æı≥È—˘µ˜≤ÈΩ·π˚£¨«Îƒ„π¿º∆Œ“–£11000√˚÷–—ß…˙º“≥§÷–”–∂‡…Ÿ√˚º“≥§≥÷∑¥∂‘è∂»£ª
£®4£©‘Ğ¥À¥Œµ˜≤ȪÓ∂Ø÷–£¨≥»˝£®1£©∞‡∫Õ≥»˝£®2£©∞‡∏˜”–2Œªº“≥§∂‘÷–—ß…˙¥¯ ÷ª˙≥÷∑¥∂‘è∂»£¨œ÷¥”÷–—°2Œªº“≥§≤Œº”—ß–£◊È÷صƒº“–£ªÓ∂Ø£¨”√¡–±Ì∑®ªÚª≠ ˜◊¥Õºµƒ∑Ω∑®«Û—°≥ˆµƒ2»À¿¥◊‘≤ªÕ¨∞‡º∂µƒ∏≈¬ £Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥ –ø™’π“ªœÓ◊‘––≥µ¬√”ŒªÓ∂Ø£¨œş¬∑–Ëæ≠A°¢B°¢C°¢DÀƒµÿ£¨»ÁÕº£¨∆‰÷–A°¢B°¢C»˝µÿ‘ĞÕ¨“ª÷±œş…œ£¨Dµÿ‘ĞAµÿ±±∆´∂´30°„∑ΩœÚ£¨‘ĞCµÿ±±∆´Œ˜45°„∑ΩœÚ£¨Cµÿ‘ĞAµÿ±±∆´∂´75°„∑ΩœÚ£Æ«“BC=CD=20km£¨Œ —ÿ…œ ˆœş¬∑¥”AµÿµΩDµÿµƒ¬∑≥Ã¥Û‘º «∂‡…Ÿ£ø£®◊Ó∫ÛΩ·π˚±£¡Ù’˚ ˝£¨≤Œøº ˝æı£∫sin15°„°÷0.25£¨cos15°„°÷0.97£¨tan15°„°÷0.27£¨![]() £©
£©

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨![]() «
«![]() µƒ÷–œş£¨
µƒ÷–œş£¨![]() £¨
£¨![]() Ωª
Ωª![]() ”е„
”е„![]() £¨
£¨![]() «
«![]() µƒ÷–µ„£¨¡¨Ω”
µƒ÷–µ„£¨¡¨Ω”![]() .
.
£®1£©«Û÷§£∫Àƒ±ş–Œ![]() «∆Ω––Àƒ±ş–Œ£ª
«∆Ω––Àƒ±ş–Œ£ª
£®2£©»ÙÀƒ±ş–Œ![]() µƒ√ʪ˝Œ™
µƒ√ʪ˝Œ™![]() £¨«Î÷±Ω”–¥≥ˆÕº÷–À˘”–√ʪ˝ «
£¨«Î÷±Ω”–¥≥ˆÕº÷–À˘”–√ʪ˝ «![]() µƒ»˝Ω«–Œ.
µƒ»˝Ω«–Œ.

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
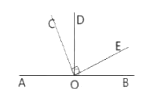
°æƒø°ø»ÁÕº£¨π˝÷±œş![]() …œ“ªµ„
…œ“ªµ„![]() £¨◊˜
£¨◊˜![]() £¨
£¨![]() £¨»Ù
£¨»Ù![]() £¨¢Ÿƒ„ªπƒİ«Û≥ˆƒƒ–©Ω«µƒ∂» ˝_____________________£®÷¡…Ÿ–¥≥ˆ¡Ω∏ˆ£¨÷±Ω«∫Õ∆ΩΩ«≥˝Õ‚£©£ª
£¨¢Ÿƒ„ªπƒİ«Û≥ˆƒƒ–©Ω«µƒ∂» ˝_____________________£®÷¡…Ÿ–¥≥ˆ¡Ω∏ˆ£¨÷±Ω«∫Õ∆ΩΩ«≥˝Õ‚£©£ª
¢Ğ”Î![]() ª•”‡µƒΩ«”–__________£¨À¸√«µƒ ˝¡øπÿœµ «________£ª”…¥Àƒ„µ√≥ˆµƒΩ·¬ğ «_____________________.
ª•”‡µƒΩ«”–__________£¨À¸√«µƒ ˝¡øπÿœµ «________£ª”…¥Àƒ„µ√≥ˆµƒΩ·¬ğ «_____________________.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº1£¨‘Ğ÷±Ω«»˝Ω«–ŒABC÷–£¨°œABC=90£¨Ω´»˝Ω«–ŒABC»∆◊≈µ„BƒÊ ±’Ζ˝◊™“ª∂®Ω«∂»µ√µΩ»˝Ω«–ŒBEF£¨EFΩªBC”е„G£Æ

£®1£©»Ù![]() £¨µ±°œABEµ»”Ğ∂‡…Ÿ∂» ±£¨
£¨µ±°œABEµ»”Ğ∂‡…Ÿ∂» ±£¨![]() £ª
£ª
£®2£©»Ù![]() £¨
£¨![]() £¨
£¨![]() £¨µ±
£¨µ±![]() ±£¨
±£¨
¢Ÿ«ÛBGµƒ≥§£ª
¢Ğ¡¨Ω”AFΩªBE”е„O£¨¡¨Ω”AE£®»ÁÕº2£©£¨…Ë»˝Ω«–ŒEOFµƒ√ʪ˝Œ™m£¨«Û»˝Ω«–ŒAEOµƒ√ʪ˝£®”√∫¨mµƒ¥˙ ˝ Ω±Ì æ£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥÷– ˝—ß ¿¥‘¥£∫ –գ∫
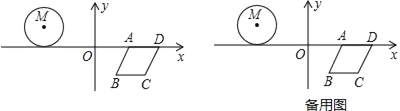
°æƒø°ø»ÁÕº£¨°—M”Ρ‚–ŒABCD‘Ğ∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨µ„Mµƒ◊¯±ÍŒ™£®©Å3£¨1£©£¨µ„Aµƒ◊¯±ÍŒ™£®2£¨0£©£¨µ„Bµƒ◊¯±ÍŒ™£®1£¨©Å![]() £©£¨µ„D‘Ğx÷·…œ£¨«“µ„D‘е„Aµƒ”“≤‡£Æ
£©£¨µ„D‘Ğx÷·…œ£¨«“µ„D‘е„Aµƒ”“≤‡£Æ
£®1£©«Û¡‚–ŒABCDµƒ÷İ≥§£ª
£®2£©»Ù°—M—ÿx÷·œÚ”““‘√ø√Î2∏ˆµ•Œª≥§∂»µƒÀŸ∂»∆Ω“∆£¨¡‚–ŒABCD—ÿx÷·œÚ◊Û“‘√ø√Î3∏ˆµ•Œª≥§∂»µƒÀŸ∂»∆Ω“∆£¨…Ë¡‚–Œ“∆∂صƒ ±º‰Œ™t£®√Σ©£¨µ±°—M”ÎADœ‡«–£¨«“«–µ„Œ™ADµƒ÷–µ„ ±£¨¡¨Ω”AC£¨«Ûtµƒ÷µº∞°œMACµƒ∂» ˝£ª
£®3£©‘Ğ£®2£©µƒÃº˛œ¬£¨µ±µ„M”ÎACÀ˘‘еƒ÷±œşµƒæ‡¿ÎŒ™1 ±£¨«Ûtµƒ÷µ£Æ
°æ¥∞∏°ø£®1£©¡‚–Œµƒ÷İ≥§Œ™8£ª£®2£©t=![]() £¨°œMAC=105°„£ª£®3£©µ±t=1©Å
£¨°œMAC=105°„£ª£®3£©µ±t=1©Å![]() ªÚt=1+
ªÚt=1+![]() ±£¨‘≤M”ÎACœ‡«–£Æ
±£¨‘≤M”ÎACœ‡«–£Æ
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®1£©π˝µ„B◊˜BE°ÕAD£¨¥π◊„Œ™E£Æ”…µ„A∫Õµ„Bµƒ◊¯±Íø…÷™£∫BE=![]() £¨AE=1£¨“¿æıπ¥π…∂®¿Ìø…«Ûµ√ABµƒ≥§£¨¥”∂¯ø…«Ûµ√¡‚–Œµƒ÷İ≥§£ª£®2£©º« M”Îx÷·µƒ«–œşŒ™F£¨ADµƒ÷–µ„Œ™E£Æœ»«Ûµ√EFµƒ≥§£¨»ª∫Û∏˘æı¬∑≥Ã= ±º‰°¡ÀŸ∂»¡–≥ˆ∑Ω≥ú¥ø…£ª∆Ω“∆µƒÕº–Œ»ÁÕº3À˘ æ£∫π˝µ„B◊˜BE°ÕAD£¨¥π◊„Œ™E£¨¡¨Ω”MF£¨FŒ™ M”ÎADµƒ«–µ„£Æ”…Ãÿ ‚»ÒΩ«»˝Ω«∫Ø ˝÷µø…«Ûµ√°œEAB=60°„£¨“¿æı¡‚–Œµƒ–‘÷ ø…µ√µΩ°œFAC=60°„£¨»ª∫Û÷§√˜°˜AFM «µ»—¸÷±Ω«»˝Ω«–Œ£¨¥”∂¯ø…µ√µΩ°œMAFµƒ∂» ˝£¨π ¥Àø…«Ûµ√°œMACµƒ∂» ˝£ª£®3£©»ÁÕº4À˘ æ£∫¡¨Ω”AM£¨π˝µ„◊˜MN°ÕAC£¨¥π◊„Œ™N£¨◊˜ME°ÕAD£¨¥π◊„Œ™E£Æœ»«Ûµ√°œMAE=30°„£¨“¿æıÃÿ ‚»ÒΩ«»˝Ω«∫Ø ˝÷µø…µ√µΩAEµƒ≥§£¨»ª∫Û“¿æı3t+2t=5-AEø…«Ûµ√tµƒ÷µ£ª»ÁÕº5À˘ æ£∫¡¨Ω”AM£¨π˝µ„◊˜MN°ÕAC£¨¥π◊„Œ™N£¨◊˜ME°ÕAD£¨¥π◊„Œ™E£Æ“¿æı¡‚–Œµƒ–‘÷ ∫Õ«–œş≥§∂®¿Ìø…«Ûµ√°œMAE=60°„£¨»ª∫Û“¿æıÃÿ ‚»ÒΩ«»˝Ω«∫Ø ˝÷µø…µ√µΩEA=
£¨AE=1£¨“¿æıπ¥π…∂®¿Ìø…«Ûµ√ABµƒ≥§£¨¥”∂¯ø…«Ûµ√¡‚–Œµƒ÷İ≥§£ª£®2£©º« M”Îx÷·µƒ«–œşŒ™F£¨ADµƒ÷–µ„Œ™E£Æœ»«Ûµ√EFµƒ≥§£¨»ª∫Û∏˘æı¬∑≥Ã= ±º‰°¡ÀŸ∂»¡–≥ˆ∑Ω≥ú¥ø…£ª∆Ω“∆µƒÕº–Œ»ÁÕº3À˘ æ£∫π˝µ„B◊˜BE°ÕAD£¨¥π◊„Œ™E£¨¡¨Ω”MF£¨FŒ™ M”ÎADµƒ«–µ„£Æ”…Ãÿ ‚»ÒΩ«»˝Ω«∫Ø ˝÷µø…«Ûµ√°œEAB=60°„£¨“¿æı¡‚–Œµƒ–‘÷ ø…µ√µΩ°œFAC=60°„£¨»ª∫Û÷§√˜°˜AFM «µ»—¸÷±Ω«»˝Ω«–Œ£¨¥”∂¯ø…µ√µΩ°œMAFµƒ∂» ˝£¨π ¥Àø…«Ûµ√°œMACµƒ∂» ˝£ª£®3£©»ÁÕº4À˘ æ£∫¡¨Ω”AM£¨π˝µ„◊˜MN°ÕAC£¨¥π◊„Œ™N£¨◊˜ME°ÕAD£¨¥π◊„Œ™E£Æœ»«Ûµ√°œMAE=30°„£¨“¿æıÃÿ ‚»ÒΩ«»˝Ω«∫Ø ˝÷µø…µ√µΩAEµƒ≥§£¨»ª∫Û“¿æı3t+2t=5-AEø…«Ûµ√tµƒ÷µ£ª»ÁÕº5À˘ æ£∫¡¨Ω”AM£¨π˝µ„◊˜MN°ÕAC£¨¥π◊„Œ™N£¨◊˜ME°ÕAD£¨¥π◊„Œ™E£Æ“¿æı¡‚–Œµƒ–‘÷ ∫Õ«–œş≥§∂®¿Ìø…«Ûµ√°œMAE=60°„£¨»ª∫Û“¿æıÃÿ ‚»ÒΩ«»˝Ω«∫Ø ˝÷µø…µ√µΩEA=![]() £¨◊Ó∫Û“¿æı3t+2t=5+AE£Æ¡–∑Ω≥ëÛΩ‚º¥ø…£Æ
£¨◊Ó∫Û“¿æı3t+2t=5+AE£Æ¡–∑Ω≥ëÛΩ‚º¥ø…£Æ
‘Ã‚Ω‚Œˆ£∫£® ![]() £©»ÁÕº1À˘ æ£∫π˝µ„
£©»ÁÕº1À˘ æ£∫π˝µ„![]() ◊˜
◊˜![]() £¨¥π◊„Œ™
£¨¥π◊„Œ™![]() £¨
£¨

°ş![]() £¨
£¨ ![]() £¨
£¨
°‡![]() £¨
£¨ ![]() £¨
£¨
°‡![]() £¨
£¨
°şÀƒ±ş–Œ![]() Œ™¡‚–Œ£¨
Œ™¡‚–Œ£¨
°‡![]() £¨
£¨
°‡¡‚–Œµƒ÷İ≥§![]() £Æ
£Æ
£®![]() £©»ÁÕº2À˘ 棨°—
£©»ÁÕº2À˘ 棨°—![]() ”Î
”Î![]() ÷·µƒ«–œşŒ™
÷·µƒ«–œşŒ™![]() £¨
£¨ ![]() ÷–µ„Œ™
÷–µ„Œ™![]() £¨
£¨

°ş![]() £¨
£¨
°‡![]() £¨
£¨
°ş![]() £¨«“
£¨«“![]() Œ™
Œ™![]() ÷–µ„£¨
÷–µ„£¨
°‡![]() £¨
£¨ ![]() £¨
£¨
°‡![]() £¨
£¨
Ω‚µ√![]() £Æ
£Æ
∆Ω“∆µƒÕº–Œ»ÁÕº3À˘ æ£∫π˝µ„![]() ◊˜
◊˜![]() £¨
£¨

¥π◊„Œ™![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨
£¨ ![]() Œ™°—
Œ™°—![]() ”Î
”Î![]() «–µ„£¨
«–µ„£¨
°ş”…£®![]() £©ø…÷™£¨
£©ø…÷™£¨ ![]() £¨
£¨ ![]() £¨
£¨
°‡![]() £¨
£¨
°‡![]() £¨
£¨
°‡![]() £¨
£¨
°şÀƒ±ş–Œ![]() «¡‚–Œ£¨
«¡‚–Œ£¨
°‡![]() £¨
£¨
°ş![]() Œ™
Œ™![]() «–œş£¨
«–œş£¨
°‡![]() £¨
£¨
°ş![]() Œ™
Œ™![]() µƒ÷–µ„£¨
µƒ÷–µ„£¨
°‡![]() £¨
£¨
°‡![]() «µ»—¸÷±Ω«»˝Ω«–Œ£¨
«µ»—¸÷±Ω«»˝Ω«–Œ£¨
°‡![]() £¨
£¨
°‡![]() £Æ
£Æ
£®![]() £©»ÁÕº4À˘ æ£∫¡¨Ω”
£©»ÁÕº4À˘ æ£∫¡¨Ω”![]() £¨π˝µ„◊˜
£¨π˝µ„◊˜![]() £¨¥π◊„Œ™
£¨¥π◊„Œ™![]() £¨◊˜
£¨◊˜![]() £¨¥π◊„Œ™
£¨¥π◊„Œ™![]() £¨
£¨

°şÀƒ±ş–Œ![]() Œ™¡‚–Œ£¨
Œ™¡‚–Œ£¨ ![]() £¨
£¨
°‡![]() £Æ
£Æ
°ş![]() °¢
°¢![]() «‘≤
«‘≤![]() µƒ«–œş
µƒ«–œş
°‡![]() £¨
£¨
°ş![]() °£
°£
°‡![]() £¨
£¨
°‡![]() £¨
£¨
°‡![]() £Æ
£Æ
»ÁÕº5À˘ æ£∫¡¨Ω”![]() £¨π˝µ„◊˜
£¨π˝µ„◊˜![]() £¨¥π◊„Œ™
£¨¥π◊„Œ™![]() £¨◊˜
£¨◊˜![]() £¨¥π◊„Œ™
£¨¥π◊„Œ™![]() £¨
£¨

°şÀƒ±ş–Œ![]() Œ™¡‚–Œ£¨
Œ™¡‚–Œ£¨ ![]() £¨
£¨
°‡![]() £¨
£¨
°‡![]() £¨
£¨
°ş![]() °¢
°¢![]() «‘≤
«‘≤![]() µƒ«–œş£¨
µƒ«–œş£¨
°‡![]() £¨
£¨
°ş![]() £¨
£¨
°‡![]() £¨
£¨
°‡![]() £¨
£¨
°‡![]() £Æ
£Æ
◊ğ…œÀ˘ ˆ£¨µ±![]() ªÚ
ªÚ![]() ±£¨‘≤
±£¨‘≤![]() ”Î
”Î![]() œ‡«–£Æ
œ‡«–£Æ
µ„涣∫¥À «“ªµ¿‘≤µƒ◊ğ∫œÃ‚.‘≤÷–µƒ∑Ω∑®πʬ…◊İΩ·£∫1°¢∑÷¿‡Ã÷¬ğÀºœÎ£∫—–æøµ„°¢÷±œş∫Õ‘≤µƒŒª÷√πÿœµ ±£¨æÕ“™¥”≤ªÕ¨µƒŒª÷√πÿœµ»•øº¬«£¨º¥“™»´√ÊΩ“ 浄°¢÷±œş∫Õ‘™µƒ∏˜÷÷ø…ƒİµƒŒª÷√πÿœµ.’‚÷÷Œª÷√πÿœµµƒøº¬«”Î∑÷Œˆ“™”√µΩ∑÷¿‡Ã÷¬ğÀºœÎ.1°¢◊™ªØÀºœÎ£∫£®1£©ªØ°∞«˙√Ê°±Œ™°∞∆Ω√Ê°±£®2£©ªØ≤ªπÊ‘ÚÕº–Œ√ʪ˝Œ™πÊ‘ÚÕº–Œµƒ√ʪ˝«ÛΩ‚.3°¢∑Ω≥ÃÀºœÎ£∫‘Ÿ”Α≤”–πÿµƒº∆À„Â÷–£¨≥˝¡À÷±Ω”‘À”√π´ ΩΩ¯––º∆À„Õ‚£¨”– ±∏˘æıÕº–ŒµƒÃÿµ„£¨¡–∑Ω≥ÃΩ‚¥£¨Àº¬∑«Â≥˛£¨π˝≥úÚΩı.
°æ–հøΩ‚¥Ã‚
°æΩ· ¯°ø
28
°æƒø°ø»ÁÕº1£¨‘Ğ∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨÷±œşl”Îx÷·°¢y÷·∑÷±Ωª”е„B£®4£¨0£©°¢C£®0£¨3£©£¨µ„AŒ™x÷·∏∫∞Î÷·…œ“ªµ„£¨AM°ÕBC”е„MΩªy÷·”е„N£®0£¨ ![]() £©£Æ“—÷™≈◊ŒÔœşy=ax2+bx+cæ≠π˝µ„A£¨B£¨C£Æ
£©£Æ“—÷™≈◊ŒÔœşy=ax2+bx+cæ≠π˝µ„A£¨B£¨C£Æ

£®1£©«Û≈◊ŒÔœşµƒ∫Ø ˝ Ω£ª
£®2£©¡¨Ω”AC£¨µ„D‘Ğœş∂ŒBC…œ∑Ωµƒ≈◊ŒÔœş…œ£¨¡¨Ω”DC£¨DB£¨»Ù°˜BCD∫Õ°˜ABC√ʪ˝¬˙◊„S°˜BCD= ![]() S°˜ABC£¨ «Ûµ„Dµƒ◊¯±Í£ª
S°˜ABC£¨ «Ûµ„Dµƒ◊¯±Í£ª
£®3£©»ÁÕº2£¨EŒ™OB÷–µ„£¨…ËFŒ™œş∂ŒBC…œ“ªµ„£®≤ª∫¨∂Àµ„£©£¨¡¨Ω”EF£Æ“ª∂ص„P¥”E≥ˆ∑¢£¨—ÿœş∂ŒEF“‘√ø√Î3∏ˆµ•ŒªµƒÀŸ∂»‘À∂صΩF£¨‘Ÿ—ÿ◊≈œş∂ŒPC“‘√ø√Î5∏ˆµ•ŒªµƒÀŸ∂»‘À∂صΩC∫ÛÕ£÷π£Æ»Ùµ„P‘Ğ’˚∏ˆ‘À∂Øπ˝≥Ã÷–”√ ±◊Ó…Ÿ£¨«Î÷±Ω”–¥≥ˆ◊Ó…Ÿ ±º‰∫Õ¥À ±µ„Fµƒ◊¯±Í£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒŞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com