
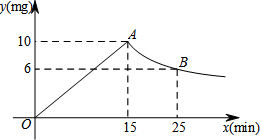
 据媒体报道,近期“甲型H7N9禽流感”可能进入发病高峰期,某校根据《学校卫生工作条例》,为预防“甲型H7N9禽流感”,对教室进行“熏药消毒”.已知药物在燃烧及释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示,第一段是线段OA,第二段是一个反比例函数的图象(即图中A点及其右侧的部分),根据图象所示信息,解答下列问题:
据媒体报道,近期“甲型H7N9禽流感”可能进入发病高峰期,某校根据《学校卫生工作条例》,为预防“甲型H7N9禽流感”,对教室进行“熏药消毒”.已知药物在燃烧及释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示,第一段是线段OA,第二段是一个反比例函数的图象(即图中A点及其右侧的部分),根据图象所示信息,解答下列问题:分析 (1)根据题意,药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,将数据代入用待定系数法可得反比例函数的关系式;
(2)利用y=2时代入反比例函数解析式,进一步求解可得答案.
解答 解:(1)设反比例函数解析式为y=$\frac{k}{x}$(k≠0),
将(25,6)代入解析式得,k=25×6=150,
则函数解析式为y=$\frac{150}{x}$(x≥15),
设正比例函数解析式为y=nx,
将A(15,10)代入上式即可求出n的值,
n=$\frac{10}{15}$=$\frac{2}{3}$,
则正比例函数解析式为y=$\frac{2}{3}$x(0≤x<15).
(2)当y=2时,$\frac{150}{x}$=2,
解得:x=75.
答:从消毒开始,师生至少在75分钟内不能进入教室.
点评 本题考查了反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两组对边分别平行 | B. | 一组对边平行,另一组对边相等 | ||
| C. | 两组对边分别相等 | D. | 一组对边平行且相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
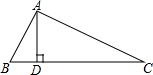 如图:在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,BD=1,AC=$2\sqrt{5}$,则AD等于( )
如图:在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,BD=1,AC=$2\sqrt{5}$,则AD等于( )| A. | 1 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com