
°æƒø°ø»ÁÕº 棨“‘’˝∑Ω–Œ![]() µƒµ„
µƒµ„![]() Œ™◊¯±Í‘≠µ„Ω®¡¢∆Ω√Ê÷±Ω«◊¯±Íœµ£¨∆‰÷–œþ∂Œ
Œ™◊¯±Í‘≠µ„Ω®¡¢∆Ω√Ê÷±Ω«◊¯±Íœµ£¨∆‰÷–œþ∂Œ![]() ‘⁄
‘⁄![]() ÷·…œ£¨œþ∂Œ
÷·…œ£¨œþ∂Œ![]() ‘⁄
‘⁄![]() ÷·…œ£¨∆‰÷–’˝∑Ω–Œ
÷·…œ£¨∆‰÷–’˝∑Ω–Œ![]() µƒ÷Ð≥§Œ™24£Æ
µƒ÷Ð≥§Œ™24£Æ
£®1£©÷±Ω”–¥≥ˆ![]() £¨
£¨![]() ¡Ωµ„µƒ◊¯±Í£Æ
¡Ωµ„µƒ◊¯±Í£Æ
£®2£©»Ù”Î![]() ÷·÷ÿ∫œµƒ÷±œþ
÷·÷ÿ∫œµƒ÷±œþ![]() “‘√ø√Î1∏ˆµ•Œª≥§∂»µƒÀŸ∂»”…
“‘√ø√Î1∏ˆµ•Œª≥§∂»µƒÀŸ∂»”…![]() ÷·œÚ”“∆Ω“∆£¨“∆∂Ø÷¡”Î
÷·œÚ”“∆Ω“∆£¨“∆∂Ø÷¡”Î![]() À˘‘⁄µƒ÷±œþ÷ÿ∫œ ±Õ£÷π£Æ‘⁄“∆∂Øπ˝≥Ã÷–÷±œþ
À˘‘⁄µƒ÷±œþ÷ÿ∫œ ±Õ£÷π£Æ‘⁄“∆∂Øπ˝≥Ã÷–÷±œþ![]() ”Î
”Î![]() °¢
°¢![]() Ωªµ„∑÷±Œ™µ„
Ωªµ„∑÷±Œ™µ„![]() ∫Õµ„
∫Õµ„![]() £ÆŒ £∫‘À∂Ø∂ý≥§ ±º‰ ±£¨≥§∑Ω–Œ
£ÆŒ £∫‘À∂Ø∂ý≥§ ±º‰ ±£¨≥§∑Ω–Œ![]() µƒ÷Ð≥§”Î≥§∑Ω–Œ
µƒ÷Ð≥§”Î≥§∑Ω–Œ![]() µƒ÷Ð≥§÷Ʊ»Œ™5£∫4£Æ
µƒ÷Ð≥§÷Ʊ»Œ™5£∫4£Æ
£®3£©‘⁄£®2£©µƒÃıº˛œ¬£¨»Ù÷±œþ![]() …œ”–“ªµ„
…œ”–“ªµ„![]() £¨¡¨Ω”
£¨¡¨Ω”![]() °¢
°¢![]() £¨«°∫√¬˙◊„
£¨«°∫√¬˙◊„![]() £Æ«Û≥ˆ
£Æ«Û≥ˆ![]() µƒ¥Û–°£Æ
µƒ¥Û–°£Æ
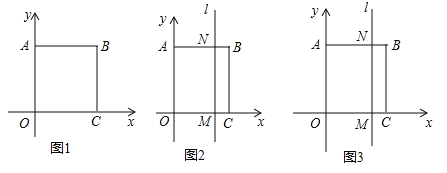
°æ¥∞∏°ø£®1£©B£®6,6£©£¨C£®6,0£©£ª£®2£©‘À∂Ø4√Î ±£¨≥§∑Ω–Œ![]() µƒ÷Ð≥§”Î≥§∑Ω–Œ
µƒ÷Ð≥§”Î≥§∑Ω–Œ![]() µƒ÷Ð≥§÷Ʊ»Œ™5£∫4£ª£®3£©
µƒ÷Ð≥§÷Ʊ»Œ™5£∫4£ª£®3£©![]() Œ™270°„ªÚ90°„ ±«°∫√
Œ™270°„ªÚ90°„ ±«°∫√![]() .
.
°æΩ‚Œˆ°ø
£®1£©∏˘æð’˝∑Ω–Œµƒ–‘÷ º¥ø…µ√µΩOA°¢OCµƒ≥§∂»”…¥Àµ√µΩµ„µƒ◊¯±Í£ª
£®2£©…Ë“∆∂Øt√Σ¨∏˘æð∆Ω“∆µ√µΩAN=OM=t£¨MN=OA=6£¨∏˘æð≥§∑Ω–Œ![]() µƒ÷Ð≥§”Î≥§∑Ω–Œ
µƒ÷Ð≥§”Î≥§∑Ω–Œ![]() µƒ÷Ð≥§÷Ʊ»Œ™5£∫4¡–≥ˆ∑Ω≥ëÛΩ‚º¥ø…µ√µΩ¥∞∏£ª
µƒ÷Ð≥§÷Ʊ»Œ™5£∫4¡–≥ˆ∑Ω≥ëÛΩ‚º¥ø…µ√µΩ¥∞∏£ª
£®3£©∑÷¡Ω÷÷«Èøˆ£∫µ„E‘⁄AB…œ∑ΩªÚœ¬∑Ω ±£¨∑÷±ª≠Õº£¨∏˘æð¥π÷±µƒ∂®“º∞’˝∑Ω–Œµƒ–‘÷ «Û÷µº¥ø….
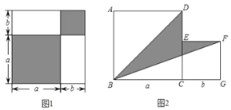
£®1£©°þÀƒ±þ–ŒABCO «’˝∑Ω–Œ£¨«“÷Ð≥§ «24£¨
°ýOA=OC=AB=BC=6£¨AB°ÕOA£¨BC°ÕOC£¨
°ýB£®6,6£©£¨C£®6,0£©£ª
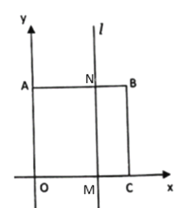
£®2£©…Ë“∆∂Øt√Σ¨
°þ”Î![]() ÷·÷ÿ∫œµƒ÷±œþ
÷·÷ÿ∫œµƒ÷±œþ![]() “‘√ø√Î1∏ˆµ•Œª≥§∂»µƒÀŸ∂»”…
“‘√ø√Î1∏ˆµ•Œª≥§∂»µƒÀŸ∂»”…![]() ÷·œÚ”“∆Ω“∆£¨
÷·œÚ”“∆Ω“∆£¨
°ýAN=OM=t£¨MN=OA=6£¨
°ýBN=CM=6-t£¨
°þ≥§∑Ω–Œ![]() µƒ÷Ð≥§”Î≥§∑Ω–Œ
µƒ÷Ð≥§”Î≥§∑Ω–Œ![]() µƒ÷Ð≥§÷Ʊ»Œ™5£∫4£¨
µƒ÷Ð≥§÷Ʊ»Œ™5£∫4£¨
°ý4£®2t+12£©=5£®12-2t+12£©£¨
Ω‚µ√t=4£¨
°ýµ±÷±œþl‘À∂Ø4√Î ±£¨≥§∑Ω–Œ![]() µƒ÷Ð≥§”Î≥§∑Ω–Œ
µƒ÷Ð≥§”Î≥§∑Ω–Œ![]() µƒ÷Ð≥§÷Ʊ»Œ™5£∫4£ª
µƒ÷Ð≥§÷Ʊ»Œ™5£∫4£ª
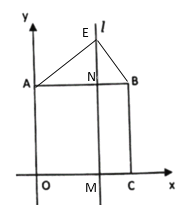
£®3£©µ±µ„E‘⁄AB…œ∑Ω ±£¨»ÁÕº£¨
°þ![]() £¨
£¨
°ý°œAEB=90°„£¨
°ý°œEAB+°œEBA=90°„£¨
°þÀƒ±þ–ŒABCO «’˝∑Ω–Œ£¨
°ý°œOAB=°œABC=90°„£¨
°ý![]() =°œOAB+°œEAB+°œABC+°œEBA=270°„£ª
=°œOAB+°œEAB+°œABC+°œEBA=270°„£ª
µ±µ„E‘⁄ABœ¬∑Ω ±£¨»ÁÕº£¨
°þ![]() £¨
£¨
°ý°œAEB=90°„£¨
°ý°œEAB+°œEBA=90°„£¨
°þÀƒ±þ–ŒABCO «’˝∑Ω–Œ£¨
°ý°œOAB=°œABC=90°„£¨
°ý![]() =°œOAB-°œEAB+°œABC-°œEBA=90°„£ª
=°œOAB-°œEAB+°œABC-°œEBA=90°„£ª
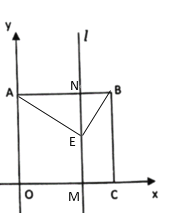
◊€…œ£¨![]() Œ™270°„ªÚ90°„ ±«°∫√
Œ™270°„ªÚ90°„ ±«°∫√![]() .
.



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄ ˝—ß—ßœ∞÷–’˚ÃÂÀºœÎ”Î◊™ªØÀºœÎ «Œ“√«≥£”√µΩµƒ ˝—ßÀºœÎ£Æ
Õº(1)÷–£¨«Û°œA+°œB+°œC+°œD+°œEµƒ∂» ˝µ»”⁄∂ý…Ÿ ±£¨Œ“√«ø…“‘¡¨Ω”CD£¨¿˚”√»˝Ω«–Œµƒƒ⁄Ω«∫Õ‘Ú”–°œB+°œE=°œECD+°œBDC£¨’‚—˘°œA°¢°œB°¢°œC°¢°œD°¢°œEµƒ∫ÕæÕ◊™ªØµΩÕ¨“ª∏ˆ°˜ACD÷–£¨º¥°œA+°œB+°œC+°œD+°œE=_____.
Õº(2)÷–°œA+°œB+°œC+°œD+°œEµƒ∂» ˝µ»”⁄______.
Õº(3)÷–°œA+°œB+°œC+°œD+°œEµƒ∂» ˝µ»”⁄________.
Õº(4)÷–°œA+°œB+°œC+°œD+°œE+°œFµƒ∂» ˝µ»”⁄________.

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø«Î»œ’Êπ€≤ÏÕº–Œ£¨Ω‚¥œ¬¡–Œ £∫
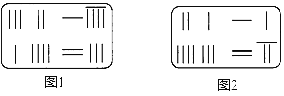
£®1£©∏˘æðÕº1÷–Ãıº˛£¨ ‘”√¡Ω÷÷≤ªÕ¨∑Ω∑®±Ì æ¡Ω∏ˆ“ı”∞Õº–Œµƒ√ʪ˝µƒ∫Õ£Æ
∑Ω∑®1£∫°° £Æ
∑Ω∑®2£∫°° £Æ
£®2£©¥”÷–ƒ„ƒÐ∑¢œ÷ ≤√¥Ω·¬€£ø«Î”√µ» Ω±Ì æ≥ˆ¿¥£∫°° £Æ
£®3£©¿˚”√£®2£©÷–Ω·¬€Ω‚戜¬√ʵƒŒ £∫»ÁÕº2£¨¡Ω∏ˆ’˝∑Ω–Œ±þ≥§∑÷±Œ™a°¢b£¨»Áπ˚a+b=10£¨ab=21£¨«Û“ı”∞≤ø∑÷µƒ√ʪ˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø°∂æ≈’¬À„ ı°∑ «Œ“π˙∂´∫∫≥ıƒÍ±ý∂©µƒ“ª≤ø ˝—ßæ≠µ‰÷¯◊˜.‘⁄À¸µƒ°∞∑Ω≥𱓪’¬¿Ô,“ª¥Œ∑Ω≥Ã◊È «”…À„≥Ô≤º÷√∂¯≥…µƒ.°∂æ≈’¬À„ ı°∑÷–µƒÀ„≥ÔÕº « ˙≈≈µƒ,œ÷‘⁄Œ“√«∞—À¸∏ƒŒ™∫·≈≈,»ÁÕº1°¢Õº2£¨Õº÷–∏˜––¥”◊ÛµΩ”“¡–≥ˆµƒÀ„≥Ô ˝∑÷±±Ì 挥÷™ ˝![]() µƒœµ ˝”Îœý”¶µƒ≥£ ˝œÓ,∞—Õº1À˘ 浃À„≥ÔÕº”√Œ“√«œ÷‘⁄À˘ Ïœ§µƒ∑Ω≥Ã◊È–Œ Ω±Ì ˆ≥ˆ¿¥æÕ «
µƒœµ ˝”Îœý”¶µƒ≥£ ˝œÓ,∞—Õº1À˘ 浃À„≥ÔÕº”√Œ“√«œ÷‘⁄À˘ Ïœ§µƒ∑Ω≥Ã◊È–Œ Ω±Ì ˆ≥ˆ¿¥æÕ «![]()
![]() ¿ýÀ∆µÿ,Õº2À˘ 浃À„≥ÔÕºŒ“√«ø…“‘”√∑Ω≥Ã◊È–Œ Ω±Ì ˆŒ™__________.
¿ýÀ∆µÿ,Õº2À˘ 浃À„≥ÔÕºŒ“√«ø…“‘”√∑Ω≥Ã◊È–Œ Ω±Ì ˆŒ™__________.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™»ÁÕº£¨![]() £¨
£¨![]() £Æ
£Æ
«Û÷§£∫![]()
÷§√˜£∫“ÚŒ™![]() (“—÷™)
(“—÷™)
À˘“‘![]() £®_______£©
£®_______£©
À˘“‘![]() __________£Æ(¡Ω÷±œþ∆Ω––£¨ƒ⁄¥ÌΩ«œýµ»)
__________£Æ(¡Ω÷±œþ∆Ω––£¨ƒ⁄¥ÌΩ«œýµ»)
“ÚŒ™![]() .(“—÷™)
.(“—÷™)
À˘“‘![]() __________£Æ£®_______£©
__________£Æ£®_______£©
À˘“‘![]() £Æ£®_______£©
£Æ£®_______£©
À˘“‘![]() £Æ(µ» Ω–‘÷ 1)
£Æ(µ» Ω–‘÷ 1)
º¥![]() £Æ
£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
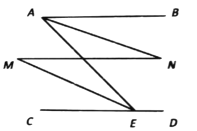
°æƒø°ø»ÁÕº£¨![]() Œ™œþ∂Œ
Œ™œþ∂Œ![]() …œ“ª∂ص„£¨∑÷±π˝µ„
…œ“ª∂ص„£¨∑÷±π˝µ„![]() ◊˜
◊˜![]() £¨
£¨![]() £¨¡¨Ω”
£¨¡¨Ω”![]() .“—÷™
.“—÷™![]() £¨…Ë
£¨…Ë![]() .
.
(1)”√∫¨![]() µƒ¥˙ ˝ Ω±Ì æ
µƒ¥˙ ˝ Ω±Ì æ![]() µƒ÷µ;
µƒ÷µ;
(2)ÃΩæø:µ±µ„![]() ¬˙◊„ ≤√¥Ãıº˛ ±£¨
¬˙◊„ ≤√¥Ãıº˛ ±£¨![]() µƒ÷µ◊Ó–°?◊Ó–°÷µ «∂ý…Ÿ?
µƒ÷µ◊Ó–°?◊Ó–°÷µ «∂ý…Ÿ?
(3)∏˘æð(2)÷–µƒΩ·¬€£¨«Îππ‘ÏÕº–Œ«Û¥˙ ˝ Ω![]() µƒ◊Ó–°÷µ.
µƒ◊Ó–°÷µ.

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨∆Ω––Àƒ±þ–ŒABCDµƒ∂‘Ω«œþAC°¢BDœýΩª”⁄µ„O£¨AE∆Ω∑÷°œBAD£¨∑÷±ΩªBC°¢BD”⁄µ„E°¢P£¨¡¨Ω”OE£¨°œADC=60°„£¨AB=![]() BC=1£¨‘Úœ¬¡–Ω·¬€£∫
BC=1£¨‘Úœ¬¡–Ω·¬€£∫
¢Ÿ°œCAD=30°„¢⁄BD=![]() ¢€S∆Ω––Àƒ±þ–ŒABCD=ABAC¢ÐOE=
¢€S∆Ω––Àƒ±þ–ŒABCD=ABAC¢ÐOE=![]() AD¢ðS°˜APO=
AD¢ðS°˜APO=![]() £¨’˝»∑µƒ∏ˆ ˝ «£®°°°°£©
£¨’˝»∑µƒ∏ˆ ˝ «£®°°°°£©

A. 2 B. 3 C. 4 D. 5
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
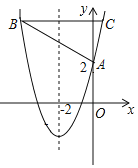
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþy=x2+bx+c”Îy÷·Ωª”⁄µ„A£®0£¨2£©£¨∂‘≥∆÷·Œ™÷±œþx=©Å2£¨∆Ω––”⁄x÷·µƒ÷±œþ”Î≈◊ŒÔœþΩª”⁄B°¢C¡Ωµ„£¨µ„B‘⁄∂‘≥∆÷·◊Û≤ý£¨BC=6£Æ
£®1£©«Û¥À≈◊ŒÔœþµƒΩ‚Œˆ Ω£Æ
£®2£©µ„P‘⁄x÷·…œ£¨÷±œþCPΩ´°˜ABC√ʪ˝∑÷≥…2£∫3¡Ω≤ø∑÷£¨«Î÷±Ω”–¥≥ˆPµ„◊¯±Í£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™¡À¡ÀΩ‚ƒ≥π´Àæ‘±π§µƒƒÍ ’»Î«Èøˆ£¨Àʪ˙≥È≤È¡Àπ´Àæ≤ø∑÷‘±π§ƒÍ ’»Î«Èøˆ≤¢ªÊ÷∆»ÁÕºÀ˘ æÕ≥º∆Õº.
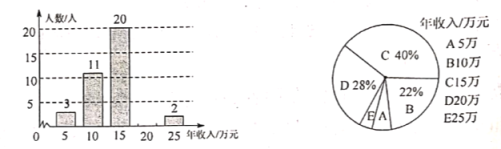
£®1£©«Î∞¥Õº÷– ˝æð≤π»´Ãı–ŒÕº£ª
£®2£©”…Õºø…÷™‘±π§ƒÍ ’»Îµƒ÷–Œª ˝ « £¨÷⁄ ˝ « £ª
£®3£©π¿º∆∏√π´À摱π§»Àæ˘ƒÍ ’»Î‘ºŒ™∂ý…Ÿ‘™£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com