
【题目】在数学学习中整体思想与转化思想是我们常用到的数学思想.
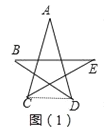
图(1)中,求∠A+∠B+∠C+∠D+∠E的度数等于多少时,我们可以连接CD,利用三角形的内角和则有∠B+∠E=∠ECD+∠BDC,这样∠A、∠B、∠C、∠D、∠E的和就转化到同一个△ACD中,即∠A+∠B+∠C+∠D+∠E=_____.
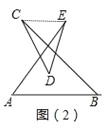
图(2)中∠A+∠B+∠C+∠D+∠E的度数等于______.
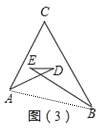
图(3)中∠A+∠B+∠C+∠D+∠E的度数等于________.
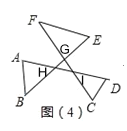
图(4)中∠A+∠B+∠C+∠D+∠E+∠F的度数等于________.

【答案】180°;180°;180°;360°.
【解析】
图(1)中,连接CD,可得∠B+∠E=∠ECD+∠BDC,故∠A+∠B+∠ACE+∠ADB+∠E=∠A+∠ACD+∠ADC=180°;
图(2)中,连接CE,可得∠A+∠B=∠AEC+∠BCE,故∠A+∠B+∠DCB+∠D+∠DEA=∠D+∠DCE+∠DEC=180°;
图(3)中,连接AB,可得∠E+∠D=∠DAB+∠EBA,故∠CAD+∠CBE+∠C+∠D+∠E=∠C+∠CAB+∠CBA=180°;
图(4)中,可得∠A+∠B=∠HGI+∠HIG,∠C+∠D=∠IHG+∠IGH,∠E+∠F=∠GHI+∠GIH,故∠A+∠B+∠C+∠D+∠E+∠F=2(∠HGI+∠HIG+∠IHG)=360°.
解:图(1)中,连接CD,
∵∠B+∠E=∠ECD+∠BDC,
∴∠A+∠B+∠ACE+∠ADB+∠E=∠A+∠ACD+∠ADC=180°;
图(2)中,连接CE,
则∠A+∠B=∠AEC+∠BCE,
∴∠A+∠B+∠DCB+∠D+∠DEA=∠D+∠DCE+∠DEC=180°;
图(3)中,连接AB,
则∠E+∠D=∠DAB+∠EBA,
∴∠CAD+∠CBE+∠C+∠D+∠E=∠C+∠CAB+∠CBA=180°;
图(4)中,∠A+∠B=∠HGI+∠HIG,∠C+∠D=∠IHG+∠IGH,∠E+∠F=∠GHI+∠GIH,
∴∠A+∠B+∠C+∠D+∠E+∠F=∠HGI+∠HIG+∠IHG+∠IGH+∠GHI+∠GIH=2(∠HGI+∠HIG+∠IHG)=360°.
故答案为:180°;180°;180°;360°.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AB为直径作⊙O交BC于点D,∠DAC=∠B.
(1)求证:AC是⊙O的切线;
(2)点E是AB上一点,若∠BCE=∠B,tan∠B=![]() ,⊙O的半径是4,求EC的长.
,⊙O的半径是4,求EC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=![]() BC,成立的个数有( )
BC,成立的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学在一次实验中统计了某一结果出现的频率,给出的统计图如图所示,则 符合这一结果的实验可能是( )

A. 掷一枚正六面体的骰子,出现6点的概率
B. 掷一枚硬币,出现正面朝上的概率
C. 任意写出一个整数,能被2整除的概率
D. 一个袋子中装着只有颜色不同,其他都相同的两个红球和一个黄球,从中任意取出一个是黄球的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知小华家、小夏家、小红家及学校在同一条大路旁,一天,他们放学后从学校出发,先向南行1000m到达小华家A处,继续向北行3000m到达小红B家处,然后向南行6000m到小夏家C处.
(1)以学校以原点,以向南方向为正方向,用1个单位长度表示1000m,请你在数轴上表示出小华家、小夏家、小红家的位置;
(2)小红家在学校什么位置?离学校有多远?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两块直角三角板的直角顶点C叠放在一起.

(1)若∠DCE=30°,求∠ACB的度数;
(2)试判断∠ACE与∠BCD的大小关系,并说明理由;
(3)猜想∠ACB与∠DCE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,BD⊥AC于点D,AD=3.5cm,点P、Q分别为AB、AD上的两个定点且BP=AQ=2cm,若在BD上有一动点E使PE+QE最短,则PE+QE的最小值为_____cm

查看答案和解析>>
科目:初中数学 来源: 题型:
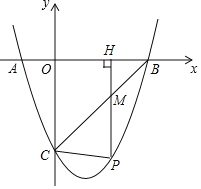
【题目】如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(﹣1,0),B(3,0)两点,与y轴相交于点C(0,﹣3).
(1)求这个二次函数的表达式;
(2)若P是第四象限内这个二次函数的图象上任意一点,PH⊥x轴于点H,与BC交于点M,连接PC.
①求线段PM的最大值;
②当△PCM是以PM为一腰的等腰三角形时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
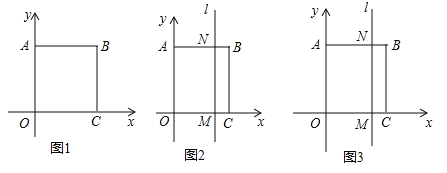
【题目】如图示,以正方形![]() 的点
的点![]() 为坐标原点建立平面直角坐标系,其中线段
为坐标原点建立平面直角坐标系,其中线段![]() 在
在![]() 轴上,线段
轴上,线段![]() 在
在![]() 轴上,其中正方形
轴上,其中正方形![]() 的周长为24.
的周长为24.
(1)直接写出![]() ,
,![]() 两点的坐标.
两点的坐标.
(2)若与![]() 轴重合的直线
轴重合的直线![]() 以每秒1个单位长度的速度由
以每秒1个单位长度的速度由![]() 轴向右平移,移动至与
轴向右平移,移动至与![]() 所在的直线重合时停止.在移动过程中直线
所在的直线重合时停止.在移动过程中直线![]() 与
与![]() 、
、![]() 交点分别为点
交点分别为点![]() 和点
和点![]() .问:运动多长时间时,长方形
.问:运动多长时间时,长方形![]() 的周长与长方形
的周长与长方形![]() 的周长之比为5:4.
的周长之比为5:4.
(3)在(2)的条件下,若直线![]() 上有一点
上有一点![]() ,连接
,连接![]() 、
、![]() ,恰好满足
,恰好满足![]() .求出
.求出![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com