【题目】如图，等边△ABC中，BD⊥AC于点D，AD＝3.5cm，点P、Q分别为AB、AD上的两个定点且BP＝AQ＝2cm，若在BD上有一动点E使PE＋QE最短，则PE＋QE的最小值为_____cm
【答案】5
【解析】
过BD作P的对称点
,连接P，Q，Q与BD交于一点E，再连接PE，根据轴对称的相关性质以及两点之间线段最短可以得出此时PE＋QE最小，并且等于Q，进一步利用全等三角形性质求解即可.
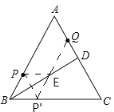
如图，过BD作P的对称点,连接P，Q，Q与BD交于一点E，再连接PE，此时PE＋QE最小.
∵与P关于BD对称，
∴PE=E，BP=B=2cm，
∴PE＋QE= Q，
又∵等边△ABC中，BD⊥AC于点D，AD＝3.5cm，
∴AC=BC=AB=7cm，
∵BP＝AQ＝2cm，
∴QC=5cm，
∵B=2cm，
∴C=5cm，
∴△Q C为等边三角形，
∴Q=5cm.
∴PE＋QE=5cm.
所以答案为5.
科目：初中数学 来源： 题型：
【题目】整式计算题
（1）先化简，再求值：（3x2﹣xy+y）﹣2（5xy﹣4x2+2y），其中x＝2，y＝1．
（2）已知小明的年龄是m岁，小红的年龄比小明的年龄的2倍少4岁，小华的年龄比小红的年龄的
还多1岁，求这三名同学的年龄的和．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD的对角线AC，BD相交于点O，将BD向两个方向延长，分别至点E和点F，且使BE=DF．
（1）求证：四边形AECF是菱形；
（2）若AC=4，BE=1，直接写出菱形AECF的边长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在数学学习中整体思想与转化思想是我们常用到的数学思想．
图(1)中，求∠A+∠B+∠C+∠D+∠E的度数等于多少时，我们可以连接CD，利用三角形的内角和则有∠B+∠E=∠ECD+∠BDC，这样∠A、∠B、∠C、∠D、∠E的和就转化到同一个△ACD中，即∠A+∠B+∠C+∠D+∠E=_____.
图(2)中∠A+∠B+∠C+∠D+∠E的度数等于______.
图(3)中∠A+∠B+∠C+∠D+∠E的度数等于________.
图(4)中∠A+∠B+∠C+∠D+∠E+∠F的度数等于________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，AB＝AC，∠BAC＝45°．若AD平分∠BAC交BC于D，BE⊥AC于E，且交A于O，连接OC．则下列说法中正确的是（ ）①AD⊥BC；②OC平分BE；③OE＝CE；④△ACD≌△BCE；⑤△OCE的周长＝AC的长度
A.①②③B.②④⑤C.①③⑤D.①③④⑤
查看答案和解析>>
科目：初中数学 来源： 题型：
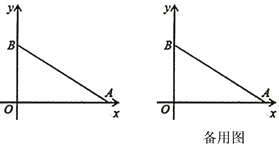
【题目】如图，在平面直角坐标系中，0为坐标原点，A、B两点的坐标分别为A(m，0)、B(0，n)，且｜m-n-3｜+
=0，点P从A出发，以每秒1个单位的速度沿射线AO匀速运动，设点P运动时间为t秒.
(1) 求OA、OB的长.
(2) 连接PB，若△POB的面积为3，求t的值.
(3) 过P作直线AB的垂线，垂足为D，直线PD与y轴交于点E，在点P运动的过程中，是否存在这样的点P，使△EOP≌△AOB?若存在，请求出t的值；若不存在，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
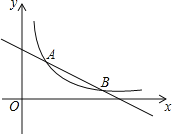
【题目】如图，已知反比例函数y=
（x＞0）的图象与一次函数y=﹣
x+4的图象交于A和B（6，n）两点．
（1）求k和n的值；
（2）若点C（x，y）也在反比例函数y=（x＞0）的图象上，求当2≤x≤6时，函数值y的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
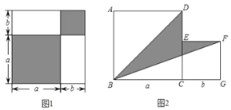
【题目】请认真观察图形，解答下列问题：
（1）根据图1中条件，试用两种不同方法表示两个阴影图形的面积的和．
方法1： ．
方法2： ．
（2）从中你能发现什么结论？请用等式表示出来： ．
（3）利用（2）中结论解决下面的问题：如图2，两个正方形边长分别为a、b，如果a+b=10，ab=21，求阴影部分的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，平行四边形ABCD的对角线AC、BD相交于点O，AE平分∠BAD，分别交BC、BD于点E、P，连接OE，∠ADC=60°，AB=
BC=1，则下列结论：
①∠CAD=30°②BD=
③S平行四边形ABCD=ABAC④OE=
AD⑤S△APO=
，正确的个数是（ ）
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com