
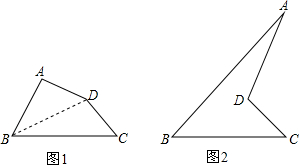
���� ��1���������������ͨ�����ı��ε�һ���Խ��ߣ����ı��ε��ڽǺ�ת��Ϊ�����ε��ڽǺ����������Խ�����ݴ˽�ɣ�
��2�����ȸ��������ε���ǵ����ʣ��ɵá�ADE=��ABE+��A����CDE=��CBE+��C��Ȼ����ݡ�ABE+��CBE=��ABC���ɵá�A+��B+��C+��D=360�㣬�ݴ˽�ɣ�
��� ��1���⣺�������������ͨ�����ı��ε�һ���Խ��ߣ�
���ı��ε��ڽǺ�ת��Ϊ�����ε��ڽǺ����������Խ����
��2��֤������ͼ2�� ��
��
���������ε���ǵ����ʣ��ɵ�
��ADE=��ABE+��A��
��CDE=��CBE+��C��
���ABE+��CBE+��A+��C=��ADE+��CDE=��ADC��
�֡ߡ�ABE+��CBE=��ABC��
���A+��B+��C=��ADC��
���A+��B+��C+��D=360�㣮
�ʴ�Ϊ���Խ��ߡ������ε��ڽǺͣ�
���� ��1��������Ҫ�����˶���ε��ڽǺͶ������Լ������ε���ǵ����ʺ�Ӧ�ã�Ҫ�������գ�������Ĺؼ���Ҫ��ȷn���ε��ڽǺ�Ϊ����n-2��•180�㣨n��3����nΪ��������
��2����������������ε��ڽǺͶ�����Ҫ�������գ�������Ĺؼ���Ҫ��ȷ�������ε��ڽǺ���180�㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��1��ͼ������Գ�ͼ��������ǣ����м����Գ��������ǣ�������������������Գ�ͼ�Σ�
��1��ͼ������Գ�ͼ��������ǣ����м����Գ��������ǣ�������������������Գ�ͼ�Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
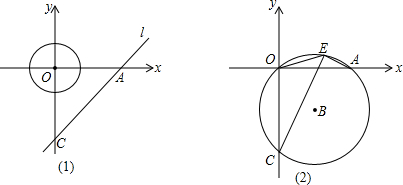
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
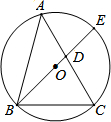 ���壺��������������Σ����������ڽǵĶ����ֱ�Ϊx�㡢y���z�㣬������x2+y2=z2��������������Ϊ���������Σ�
���壺��������������Σ����������ڽǵĶ����ֱ�Ϊx�㡢y���z�㣬������x2+y2=z2��������������Ϊ���������Σ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com