
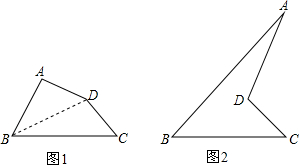
 (1)图①是轴对称图形吗?如果是,它有几条对称轴?如果不是,可以怎样把它补成轴对称图形?
(1)图①是轴对称图形吗?如果是,它有几条对称轴?如果不是,可以怎样把它补成轴对称图形?科目:初中数学 来源: 题型:解答题
| A型 | B型 | |
| 价格(万元/台) | a | b |
| 处理污水量(吨/月) | 250 | 200 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
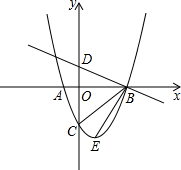 如图,抛物线y=ax2+bx-3,顶点为E,该抛物线与x轴交于A,B两点,与y轴交于点C,且OB=OC=3OA.直线$y=-\frac{1}{3}x+1$与y轴交于点D.求∠DBC-∠CBE.
如图,抛物线y=ax2+bx-3,顶点为E,该抛物线与x轴交于A,B两点,与y轴交于点C,且OB=OC=3OA.直线$y=-\frac{1}{3}x+1$与y轴交于点D.求∠DBC-∠CBE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
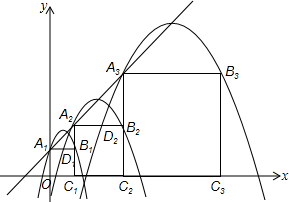 在平面直角坐标系中xOy中,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图的方式放置.点A1,A2,A3…、An和点C1,C2,C3…、Cn分别落在直线y=x+1和x轴上.抛物线L1过点A1、B1,且顶点在直线y=x+1上,抛物线L2过点A2、B2,且顶点在直线y=x+1上,…,按此规律,抛物线Ln过点An、Bn,且顶点也在直线y=x+1上,其中抛物线L1交正方形A1B1C1O的边A1B1于点D1,抛物线L2交正方形A2B2C2C1的边A2B2于点D2…,抛物线Ln交正方形AnBnCnCn-1的边AnBn于点Dn(其中n≥2且n为正整数).
在平面直角坐标系中xOy中,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图的方式放置.点A1,A2,A3…、An和点C1,C2,C3…、Cn分别落在直线y=x+1和x轴上.抛物线L1过点A1、B1,且顶点在直线y=x+1上,抛物线L2过点A2、B2,且顶点在直线y=x+1上,…,按此规律,抛物线Ln过点An、Bn,且顶点也在直线y=x+1上,其中抛物线L1交正方形A1B1C1O的边A1B1于点D1,抛物线L2交正方形A2B2C2C1的边A2B2于点D2…,抛物线Ln交正方形AnBnCnCn-1的边AnBn于点Dn(其中n≥2且n为正整数).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com