
分析 各项方程整理为一般形式,找出二次项,一次项,以及常数项即可.
解答 解:(1)方程整理得:x2-121=0,
二次项为x2,一次项为0,常数项为-121;
(2)方程整理得:x2-2x-11=0,
二次项为x2,一次项为-2x,常数项为-11;
(3)方程整理得:x2-x-2=0,
二次项为x2,一次项为-x,常数项为-2;
(4)方程整理得:6x2-7x-21=0,
二次项为6x2,一次项为-7x,常数项为-21.
点评 此题考查了一元二次方程的一般形式,一元二次方程的一般形式是:ax2+bx+c=0(a,b,c是常数且a≠0)特别要注意a≠0的条件.这是在做题过程中容易忽视的知识点.在一般形式中ax2叫二次项,bx叫一次项,c是常数项.其中a,b,c分别叫二次项系数,一次项系数,常数项.


科目:初中数学 来源: 题型:填空题
 为鼓励学生课外阅读,某校制定了“阅读奖励方案”.方案公布后,随机征求了100名学生的意见,并对持“赞成”、“反对”、“弃权”三种意见的人数进行统计,绘制成如图所示的扇形图,则赞成该方案所对应扇形的圆心角的度数为252°.
为鼓励学生课外阅读,某校制定了“阅读奖励方案”.方案公布后,随机征求了100名学生的意见,并对持“赞成”、“反对”、“弃权”三种意见的人数进行统计,绘制成如图所示的扇形图,则赞成该方案所对应扇形的圆心角的度数为252°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,BC:AB=1:2,延长AB到点B,使AB1=2AB,延长AC到点C1,使AC1=2AC,则sin∠AB1C1的值是( )
如图,BC:AB=1:2,延长AB到点B,使AB1=2AB,延长AC到点C1,使AC1=2AC,则sin∠AB1C1的值是( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 无法判断 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)图①是轴对称图形吗?如果是,它有几条对称轴?如果不是,可以怎样把它补成轴对称图形?
(1)图①是轴对称图形吗?如果是,它有几条对称轴?如果不是,可以怎样把它补成轴对称图形?查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
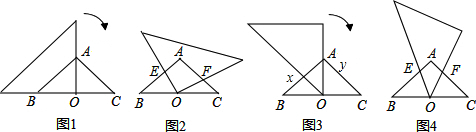
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com