
分析 (1)根据实数运算的运算顺序,从左向右依次计算即可.
(2)根据实数运算的运算顺序,首先计算开方,然后从左向右依次计算即可.
解答 解:(1)3$\sqrt{3}$+2$\sqrt{3}$-6$\sqrt{3}$
=5$\sqrt{3}$-6$\sqrt{3}$
=-$\sqrt{3}$;
(2)|$\sqrt{3}$-2|+$\root{3}{-8}$+$\sqrt{(-2)^{2}}$-|-2|
=2-$\sqrt{3}-2+2-2$
=-$\sqrt{3}$.
点评 此题主要考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到有的顺序进行.另外,有理数的运算律在实数范围内仍然适用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
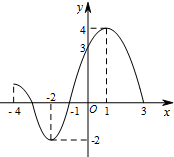 已知某函数图象如图所示,请回答下列问题:
已知某函数图象如图所示,请回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com