
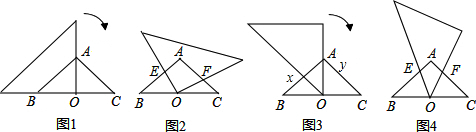
���� ��1����������AO������ȫ���������ж��ķ������жϳ���AOE�ա�COF�������жϳ�AE=CF��Ȼ�����AE=AB-BE�����y��x�ĺ�������ʽ����д��x��ȡֵ��Χ���ɣ�
��2�������dz���O����ת�Ĺ����У���OEF�ܹ��ɵ���ֱ�������Σ��ٵ�F��A�غ�ʱ��x=0����ʱOE=EF���ڵ�E��A�غ�ʱ��x=2����ʱOE=OF��
��3�������ȸ��������������ж��ķ������жϳ���BEO�ס�COF�������жϳ�$\frac{BE}{CO}=\frac{BO}{CF}$��Ȼ����Rt��ABC�У��ֱ����BC��BO��C0��ֵ���Ƕ��٣������жϳ�y��x�ĺ�������ʽ���Լ�x��ȡֵ��Χ��
�ڽ����dz���O����ת��ͼ4���Ĺ����У���OEF�ܹ��ɵ��������Σ���F��A�غ�ʱ��x=1����ʱOE=EF����E��A�غ�ʱ��x=2����ʱEF=OF����E��F�ֱ���A�������ʱ��x=$\sqrt{2}$����ʱOE=OF��
��� �⣺��1����ͼ2������AO��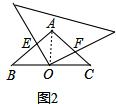 ��
��
��AB=AC����BAC=90�㣬
���ABCΪ����ֱ�������Σ���B=��C=45�㣬
�ߵ�OΪBC���е㣬
���AOC=90�㣬��EAO=��C=45�㣬AO=CO��
�ߡ�EOA+��AOF=90�㣬��COF+��AOF=90�㣬
���EOA=��FOC��
�ڡ�AOE�͡�COF�У�
$\left\{\begin{array}{l}{��EAO=��FCO=45��}\\{AO=CO}\\{��EOA=��FOC}\end{array}\right.$
���AOE�ա�COF��
��AE=CF��
��y=2-x��0��x��2����
��2�������dz���O����ת�Ĺ����У���OEF�ܹ��ɵ���ֱ�������Σ�
�ٵ�F��A�غ�ʱ��x=0����ʱOE=EF��
�ڵ�E��A�غ�ʱ��x=2����ʱOE=OF��
�ۡߡ�EOF=90�㣬
��OF=EF�����ܳ�����
��3������ͼ3������AO�� ��
��
��AB=AC����BAC=90�㣬
���ABCΪ����ֱ�������Σ���B=��C=45�㣬
���BEO+��EOB=135�㣬
�ߡ�EOF=45�㣬
���FOC+��EOB=180��-45��=135�㣬
���BEO=��FOC��
�ڡ�BEO�͡�COF�У�
$\left\{\begin{array}{l}{��B=��C=45��}\\{��BEO=��FOC}\end{array}\right.$
���BEO�ס�COF��
��$\frac{BE}{CO}=\frac{BO}{CF}$��
��Rt��ABC��
BC=$\sqrt{{AB}^{2}{+AC}^{2}}$=$\sqrt{{2}^{2}{+2}^{2}}$=2$\sqrt{2}$��
�ߵ�OΪBC���е㣬
��BO=C0=$\sqrt{2}$��
��BE=x��CF=y��
��$\frac{x}{\sqrt{2}}=\frac{\sqrt{2}}{y}$��
��xy=2��
��y=$\frac{2}{x}��1��x��2��$��
�ڽ����dz���O����ת�Ĺ����У���OEF�ܹ��ɵ��������Σ�
��F��A�غ�ʱ��x=1����ʱOE=EF��
��E��A�غ�ʱ��x=2����ʱEF=OF��
��E��F�ֱ���A�������ʱ��x=$\sqrt{2}$����ʱOE=OF��
���� ��1��������Ҫ�����˼��α任�ۺ��⣬�����˷������������������˷�������˼���Ӧ�ã����������ν��˼���Ӧ�ã�
��2�����������ȫ�������ε��ж���Ҫ�������գ�������Ĺؼ���Ҫ��ȷ�����ж�����1��SSS--�����߷ֱ��Ӧ��ȵ�����������ȫ�ȣ����ж�����2��SAS--������нǷֱ��Ӧ��ȵ�����������ȫ�ȣ����ж�����3��ASA--���Ǽ���б߷ֱ��Ӧ��ȵ�����������ȫ�ȣ����ж�����4��AAS--���Ǽ�����һ���ǵĶԱ߶�Ӧ��ȵ�����������ȫ�ȣ����ж�����5��HL--б����ֱ�DZ߶�Ӧ��ȵ�����ֱ��������ȫ�ȣ�
��3����������˵����������Լ�����ֱ�������ε����ʺ�Ӧ�ã�Ҫ�������գ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
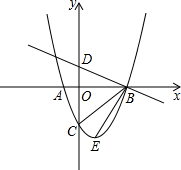 ��ͼ��������y=ax2+bx-3������ΪE������������x�ύ��A��B���㣬��y�ύ�ڵ�C����OB=OC=3OA��ֱ��$y=-\frac{1}{3}x+1$��y�ύ�ڵ�D�����DBC-��CBE��
��ͼ��������y=ax2+bx-3������ΪE������������x�ύ��A��B���㣬��y�ύ�ڵ�C����OB=OC=3OA��ֱ��$y=-\frac{1}{3}x+1$��y�ύ�ڵ�D�����DBC-��CBE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
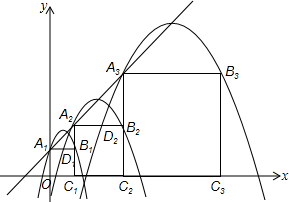 ��ƽ��ֱ������ϵ��xOy�У�������A1B1C1O��A2B2C2C1��A3B3C3C2����������ͼ�ķ�ʽ���ã���A1��A2��A3����An�͵�C1��C2��C3����Cn�ֱ�����ֱ��y=x+1��x���ϣ�������L1����A1��B1���Ҷ�����ֱ��y=x+1�ϣ�������L2����A2��B2���Ҷ�����ֱ��y=x+1�ϣ��������˹��ɣ�������Ln����An��Bn���Ҷ���Ҳ��ֱ��y=x+1�ϣ�����������L1��������A1B1C1O�ı�A1B1�ڵ�D1��������L2��������A2B2C2C1�ı�A2B2�ڵ�D2����������Ln��������AnBnCnCn-1�ı�AnBn�ڵ�Dn������n��2��nΪ����������
��ƽ��ֱ������ϵ��xOy�У�������A1B1C1O��A2B2C2C1��A3B3C3C2����������ͼ�ķ�ʽ���ã���A1��A2��A3����An�͵�C1��C2��C3����Cn�ֱ�����ֱ��y=x+1��x���ϣ�������L1����A1��B1���Ҷ�����ֱ��y=x+1�ϣ�������L2����A2��B2���Ҷ�����ֱ��y=x+1�ϣ��������˹��ɣ�������Ln����An��Bn���Ҷ���Ҳ��ֱ��y=x+1�ϣ�����������L1��������A1B1C1O�ı�A1B1�ڵ�D1��������L2��������A2B2C2C1�ı�A2B2�ڵ�D2����������Ln��������AnBnCnCn-1�ı�AnBn�ڵ�Dn������n��2��nΪ�����������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | $\frac{1}{2}$ | C�� | -1 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com