
分析 (1)AB与坐标轴平行,则AB的长为两点的纵坐标之差;
(2)①先解方程组得到b-a=2,则根据梯形的面积公式可计算出四边形ACDB的面积=9;
②分类讨论:当a>0,S△OAB=S△OBD-S△OAC-S梯形ACDB=$\frac{3}{2}$a-3,则6<$\frac{3}{2}$a-3<10,解得6<a<$\frac{26}{3}$;当a<0,b>0,S△OAB=S梯形ACDB-S△OBD-S△OAC=3-$\frac{3}{2}$a,则6<3-$\frac{3}{2}$a<10,解得-$\frac{14}{3}$<a<-2,而b=2+a>0,则a>-2,故舍去;当a<0,b<0,S△OAB=S△OBD+S梯形ACDB-S△OAC=3-$\frac{3}{2}$a,则6<3-$\frac{3}{2}$a<10,解得-$\frac{14}{3}$<a<-2,于是得到a的取值范围为6<a<$\frac{26}{3}$或-$\frac{14}{3}$<a<-2.
解答 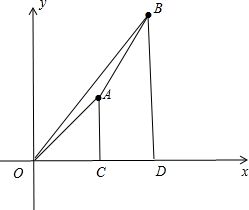 解:(1)∵AB与坐标轴平行,即AB平行于y轴,
解:(1)∵AB与坐标轴平行,即AB平行于y轴,
∴AB=6-3=3;
(2)①由方程组$\left\{\begin{array}{l}a+3b-4c=2\\ a-2b+c=-3\end{array}\right.$得b-a=2,
∵AC⊥x轴,垂足为C,BD⊥x轴,垂足为D,
∴C(a,0),D(b,0),如图,
∴四边形ACDB的面积=$\frac{1}{2}$•(3+6)•(b-a)=$\frac{1}{2}$•9•2=9;
②当a>0,
∵S△OAB=S△OBD-S△OAC-S梯形ACDB,
∴S△OAB=$\frac{1}{2}$•6•b-$\frac{1}{2}$•3•a-9=3b-$\frac{3}{2}$a-9,
而b=2+a,
∴S△OAB=3(2+a)-$\frac{3}{2}$a-9=S△OAB=$\frac{3}{2}$a-3,
∴6<$\frac{3}{2}$a-3<10,解得6<a<$\frac{26}{3}$;
当a<0,b>0,
S△OAB=S梯形ACDB-S△OBD-S△OAC=9-$\frac{1}{2}$•6•b+$\frac{1}{2}$•3•a=9-3b+$\frac{3}{2}$a=9-3(2+a)+$\frac{3}{2}$a=3-$\frac{3}{2}$a
∴6<3-$\frac{3}{2}$a<10,解得-$\frac{14}{3}$<a<-2,
而b=2+a>0,则a>-2,故舍去,
当a<0,b<0,
∵S△OAB=S△OBD+S梯形ACDB-S△OAC=-$\frac{1}{2}$•6•b+9+$\frac{1}{2}$•3•a=-3b+9+$\frac{3}{2}$a=-3(2+a)+9+$\frac{3}{2}$a=3-$\frac{3}{2}$a
∴6<3-$\frac{3}{2}$a<10,解得-$\frac{14}{3}$<a<-2,
综上所述,a的取值范围为6<a<$\frac{26}{3}$或-$\frac{14}{3}$<a<-2.
点评 本题考查了坐标与图形性质:利用点的坐标求相应线段的长和判断线段与坐标轴的位置关系.也考查了三角形面积公式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
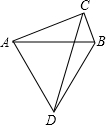 如图,以线段AB为边分别作直角三角形ABC和等边三角形ABD,其中∠ACB=90°.连接CD,当CD的长度最大时,此时∠CAB的大小是( )
如图,以线段AB为边分别作直角三角形ABC和等边三角形ABD,其中∠ACB=90°.连接CD,当CD的长度最大时,此时∠CAB的大小是( )| A. | 75° | B. | 45° | C. | 30° | D. | 15° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{35-25=y}\\{45(x-2)=y-25}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{35x=y-25}\\{45(x-2)+25=y}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{35x+25=y}\\{45(x-1)+25=y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{35x=y+25}\\{y-45(x-2)=25}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A型 | B型 | |
| 价格(万元/台) | a | b |
| 处理污水量(吨/月) | 250 | 200 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
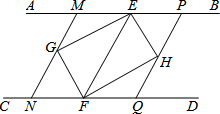 如图,AB∥CD,点E、F分别在AB、CD上,连接EF,∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H.
如图,AB∥CD,点E、F分别在AB、CD上,连接EF,∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
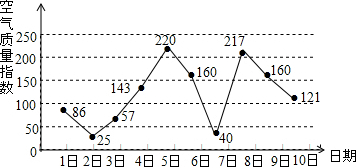 如图,气象局预报某市6月10日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示重度污染.某人随机选择6月1日至6月8日中的某一天到达该市,并连续停留3天,则此人在该市停留期间遇到空气为重度污染的概率是$\frac{3}{4}$.
如图,气象局预报某市6月10日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示重度污染.某人随机选择6月1日至6月8日中的某一天到达该市,并连续停留3天,则此人在该市停留期间遇到空气为重度污染的概率是$\frac{3}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com