
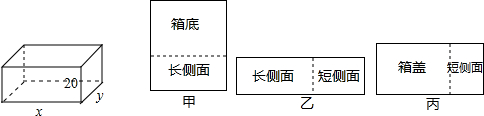
分析 (1)利用展开图结合立体图形的边长进而得出答案;
(2)利用“甲块木板的面积比丙块木板的面积大300平方厘米,乙块木板面积为1500平方厘米”,结合(1)中所求得出等式求出即可;
(3)利用(1)中所求表示出箱子的侧面积,进而利用木板的利用率为$\frac{4}{5}$,得出等式求出即可.
解答 解:(1)由图可得:甲,xy+20x;乙:20x+20y;丙:xy+20y;
(2)由题意可得:$\left\{\begin{array}{l}{xy+20x-(xy+20y)=300}\\{20(x+y)=1500}\end{array}\right.$,
即$\left\{\begin{array}{l}{x-y=15}\\{x+y=75}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=45}\\{y=30}\end{array}\right.$,
故体积为:V=20xy=27000(cm3);
(3)由题意可得:$\frac{2xy+40(x+y)}{100(x+y)}$=$\frac{4}{5}$,
∴xy=20(x+y),
∴$\frac{xy}{x+y}$=20.
点评 此题主要考查了二元一次方程组的应用以及分式方程的应用,正确利用已知得出等量关系是解题关键.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:解答题
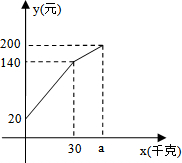 一农民带上若干千克自产的西红柿进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的西红柿千克数x与他手中持有的钱数y(含备用零钱)的关系,如图所示,结合图象回答下列问题.
一农民带上若干千克自产的西红柿进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的西红柿千克数x与他手中持有的钱数y(含备用零钱)的关系,如图所示,结合图象回答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com