
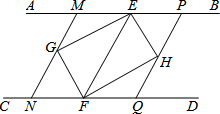
 如图,AB∥CD,点E、F分别在AB、CD上,连接EF,∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H.
如图,AB∥CD,点E、F分别在AB、CD上,连接EF,∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H.分析 (1)利用角平分线的定义结合平行线的性质得出∠FEH+∠EFH=90°,进而得出∠GEH=90°,进而求出四边形EGFH是矩形;
(2)利用菱形的判定方法首先得出要证?MNQP是菱形,只要证MN=NQ,再证∠MGE=∠QFH得出即可
解答 (1)证明:∵EH平分∠BEF,
∴∠FEH=$\frac{1}{2}$∠BEF,
∵FH平分∠DFE,
∴∠EFH=$\frac{1}{2}$∠DFE,
∵AB∥CD,
∴∠BEF+∠DFE=180°,
∴∠FEH+∠EFH=$\frac{1}{2}$(∠BEF+∠DFE)=$\frac{1}{2}$×180°=90°,
∵∠FEH+∠EFH+∠EHF=180°,
∴∠EHF=180°-(∠FEH+∠EFH)=180°-90°=90°,
同理可得:∠EGF=90°,
∵EG平分∠AEF,
∴∠EFG=$\frac{1}{2}$∠AEF,
∵EH平分∠BEF,
∴∠FEH=$\frac{1}{2}$∠BEF,
∵点A、E、B在同一条直线上,
∴∠AEB=180°,
即∠AEF+∠BEF=180°,
∴∠FEG+∠FEH=$\frac{1}{2}$(∠AEF+∠BEF)=$\frac{1}{2}$×180°=90°,
即∠GEH=90°
∴四边形EGFH是矩形;
(2)解:答案不唯一:
由AB∥CD,MN∥EF,PQ∥EF,易证四边形MNQP是平行四边形,
要证?MNQP是菱形,只要证MN=NQ,由已知条件:FG平分∠CFE,MN∥EF,
故只要证GM=FQ,即证△MGE≌△QFH,易证 GE=FH、∠GME=∠FQH.
故只要证∠MGE=∠QFH,易证∠MGE=∠GEF,∠QFH=∠EFH,∠GEF=∠EFH,即可得证;
故答案为:FG平分∠CFE,GE=FH、∠GME=∠FQH,∠GEF=∠EFH.
点评 此题主要考查了矩形的判定以及菱形的判定和角平分线的性质,根据题意得出证明菱形的方法是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com