
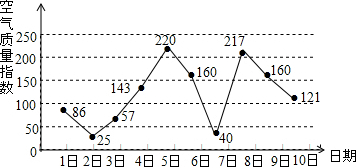
 如图,气象局预报某市6月10日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示重度污染.某人随机选择6月1日至6月8日中的某一天到达该市,并连续停留3天,则此人在该市停留期间遇到空气为重度污染的概率是$\frac{3}{4}$.
如图,气象局预报某市6月10日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示重度污染.某人随机选择6月1日至6月8日中的某一天到达该市,并连续停留3天,则此人在该市停留期间遇到空气为重度污染的概率是$\frac{3}{4}$. 分析 首先分别判断出6月1日至6月8日这8天中,有几天使得此人在该市停留期间遇到空气为重度污染,然后根据概率公式,求出此人在该市停留期间遇到空气为重度污染的概率是多少即可.
解答 解:此人6月3日-6月8日的这6天中的任意一天到达该市,
在该市停留期间都能遇到空气为重度污染,
所以此人在该市停留期间遇到空气为重度污染的概率是:
6÷8=$\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 (1)此题主要考查了概率公式的应用,要熟练掌握,解答此题的关键是要明确:随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数.
(2)此题还考查了折线统计图的性质和应用,要熟练掌握,解答此题的关键是要明确:折线图不但可以表示出数量的多少,而且能够清楚地表示出数量的增减变化情况.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:选择题
| A. | k>-$\frac{1}{2}$ | B. | k<-$\frac{1}{2}$ | C. | k=$\frac{1}{2}$ | D. | k=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
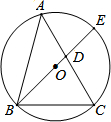 定义:对于任意的三角形,设其三个内角的度数分别为x°、y°和z°,若满足x2+y2=z2,则称这个三角形为勾股三角形.
定义:对于任意的三角形,设其三个内角的度数分别为x°、y°和z°,若满足x2+y2=z2,则称这个三角形为勾股三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com