
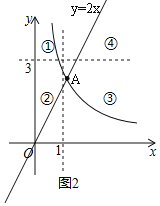
����Ŀ����ͼ1�����ε�һ���߳�Ϊx���ܳ���һ��Ϊy�����壨x��y��Ϊ������ε����ꡣ��ͼ2����ƽ��ֱ������ϵ�У�ֱ��x=1��y=3����һ�����ֳ�4��������֪����1������Ķ�Ӧ��A������ͼ��ʾ��˫�����ϣ�����2������Ķ�Ӧ������������У���������������ȷ������ ��

A. ��A�ĺ������п��ܴ���3
B. ����1��������ʱ����Aλ�������
C. ����A��˫���������ƶ�ʱ������1�������С
D. ����Aλ�������ʱ������1���ܺ;���2ȫ��
���𰸡�D
��������
A�����ݷ���������kһ����������ͼ�εã���x=1ʱ��y��3����k=xy��3����Ϊy�Ǿ����ܳ���һ�룬��y��x�����жϵ�A�ĺ����겻���ܴ���3��
B�����������α߳���ȵã�y=2x���õ�A��ֱ��y=2x��˫���ߵĽ��㣬��ͼ����ͼ2������A������ۣ������жϣ�
C���ȱ�ʾ�������S=x��y-x��=xy-x2=k-x2������A��˫���������ƶ�ʱ��x��ֵ��Խ��ԽС������1�������Խ��Խ�����жϣ�
D������Aλ������٣���x��1����һ��Ϊ��y-x��2������2������Ķ�Ӧ������������еã�x��1��y��3������һ��y-x��0�������жϣ�
��ͼ�����A��x��y����
A���跴������������ʽΪ��y=![]() ��k��0����
��k��0����
��ͼ�ο�֪����x=1ʱ��y��3��
��k=xy��3��
��y��x��
��x��3������A�ĺ����겻���ܴ���3��
��ѡ��A����ȷ��
B��������1Ϊ������ʱ���߳�Ϊx��y=2x��
���A��ֱ��y=2x��˫���ߵĽ��㣬��ͼ2������A���������
��ѡ��B����ȷ��
C����һ��Ϊx������һ��Ϊy-x��S=x��y-x��=xy-x2=k-x2��
�ߵ���A��˫���������ƶ�ʱ��x��ֵ��Խ��ԽС��
�����1�������Խ��Խ��
��ѡ��C����ȷ��
D������Aλ�������ʱ��
�ߵ�A��x��y����
��x��1��y��3������һ��Ϊ��y-x��2��
����2����������У�x��1��y��3������һ��y-x��0��
�൱��Aλ�������ʱ������1���ܺ;���2ȫ�ȣ�
��ѡ�����ȷ��
��ѡD��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�У�AB��6��AD��8����E�DZ�AD��һ�㣬EM��BC��AB�ڵ�M����N������MB�ϣ���AE��AM��AN�ı������
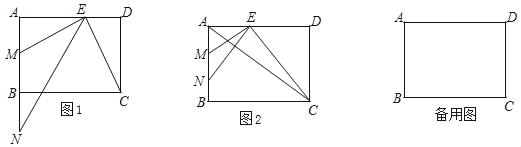
��1����ͼ1����֤����ANE����DCE��
��2����ͼ2������N���߶�MB֮�䣬����AC����AC��NE���ഹֱ����MN�ij���
��3������AC�������AEC���Ե�E��M��NΪ��������ɵ����������ƣ���DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס����������̶Ӽƻ���һ����18ǧ����幫·����֪���̶ӱ��ҹ��̶�ÿ�����·0.6ǧ�ף��ҹ��̶ӵ��������·�������������Ǽ��̶ӵ��������·��������������1.5����
��1����ס����������̶�ÿ�����·����ǧ�ף�
��2�������̶�ÿ�����·����Ϊ0.6��Ԫ���ҹ��̶�ÿ�����·����Ϊ0.5��Ԫ��Ҫʹ�������̶���·�ܷ��ò�����6.3��Ԫ�����̶�������·�����죿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�������y��ax2+bx+c������A����2��0����B��4��0����C��0��3�����㣮
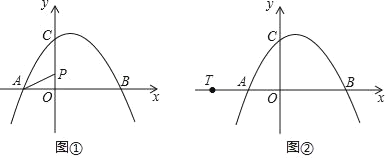
��1�����������ߵĽ���ʽ��
��2����P��y���ϵ�һ�����㣬����PA������5PA+4PC����Сֵ��
��3����ͼ�ڣ���ֱ��l������T����4��0����QΪֱ��l�ϵĶ��㣬����A��B��QΪ����������ֱ�����������ҽ�������ʱ������ֱ��l�Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ߵĶ���ΪA��1��4������������y�ύ�ڵ�B��0��3������x�ύ��C��D���㣮��P��x���ϵ�һ�����㣮
��1����������ߵĽ���ʽ��
��2����C��D�������꼰��BCD�������
��3������P��x���Ϸ����������ϣ�����S��PCD=![]() S��BCD�����P�����꣮
S��BCD�����P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ABCD�У�AD��BC��AB��AC��E�DZ�BC�ϵĵ㣬�ҡ�AED����CAD��DE��AC�ڵ�F��
��1����֤����ABE�ס�DAF��
��2����ACFC��AEECʱ����֤��AD��BE��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
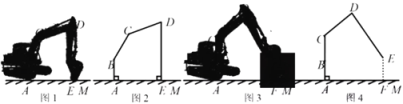
����Ŀ��ij�ھ���ĵ�����AB=0.8�ף�����BC=1.2�ף�CD=1.5�ף�BC��CD�Ĺ̶��нǡ�BCD=140������ʼλ����ͼ1,���˶���D���������E����ֱ��DE��ֱ����AM�ڵ�E����á�CDE=70��(ʾ��ͼ2)������ʱ��ͼ3������BC���Ƶ�Bת��������A��B��C��ͬһֱ��ʱ�����˶���D������ߵ�(ʾ��ͼ4)��
(1)���ھ���ڳ�ʼλ��ʱ����BC��AB�ļнǡ�ABC�Ķ�����
(2)�ʶ��˶���D����ߵ�ȳ�ʼλ�ø��˶�����(��ȷ��0.1��)?
�������ݣ�sin50���0.77��cos50���0.64��sin70���0.94��cos70���0.34��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ���ִ����е� B ��ʱ�����С�� A �ڴ��ı�ƫ�� 60��ķ����ִ��� B ������������������ 20 ���ﵽ�� C ��ʱ�����С�� A �ڱ����ı�ƫ�� 30��ķ���
��1����С�� A �������ִ�����·�� BC �ľ����� AD���� AD �ij���
��2����֪��С����Χ 17 �������а��������ִ����ı亽�������ǰ��ʻ�������ִ���������Σ�գ���![]() ��1.732��
��1.732��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ���ų�Ա��������ѧ��֪ʶ����ij����ƵĿ���![]() ͼ���߶�MN�ij�
ͼ���߶�MN�ij�![]() ��ֱ��MN��ֱ�ڵ��棬����Ϊ��
��ֱ��MN��ֱ�ڵ��棬����Ϊ��![]() �ڵ���A����õ�M������Ϊ
�ڵ���A����õ�M������Ϊ![]() ����N������Ϊ
����N������Ϊ![]() ����B����õ�M������Ϊ
����B����õ�M������Ϊ![]() ��
��![]() �ף���A��B��P������һֱ����
�ף���A��B��P������һֱ����![]() ������������������ƵĿ�MN�ij���
������������������ƵĿ�MN�ij���
![]() �ο����ݣ�
�ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com