
分析 首先设出四个数字,规定它们大小,由题意得出四个方程,利用巧算得出结果.
解答 解:设四个数分别为a、b、c、d,且规定a>b>c>d,
则由题意得:$\left\{\begin{array}{l}{a+b+c=56}\\{a+b+d=22}\\{a+c+d=18}\\{b+c+d=6}\end{array}\right.$,
四个式子相加得:
3(a+b+c+d)=102,
∴a+b+c+d=34,
∴(a+b+c+d)-(b+c+d)=34-6
∴a=28.
故答案为:28.
点评 题目考查了有理数的大小比较.题目巧妙地将有理数的大小比较和四元一次方程组结合,考查学生的观察和理解能力.学生应注意在解题过程中利用巧算简化运算过程.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:填空题
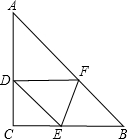 如图,在等腰直角三角形ABC中,AC=BC=2,∠C=90°,将△ABC折叠,使顶点B落在线段AC上的点D处,折痕为EF,如果△DEF为等腰三角形,则BE的长为4-2$\sqrt{2}$或1或2.
如图,在等腰直角三角形ABC中,AC=BC=2,∠C=90°,将△ABC折叠,使顶点B落在线段AC上的点D处,折痕为EF,如果△DEF为等腰三角形,则BE的长为4-2$\sqrt{2}$或1或2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
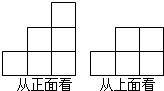 由若干个(大于8个)大小相同的正方体组成一个几何体的从正面看和从上面看如图所示,则这个几何体的从左面看不可能是下列图中的( )
由若干个(大于8个)大小相同的正方体组成一个几何体的从正面看和从上面看如图所示,则这个几何体的从左面看不可能是下列图中的( )| A. |  | B. |  | C. |  | D. | 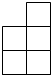 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ax2+bx+c=0 | B. | 2x2-3x+4=x2 | C. | x+3=$\frac{1}{x}$ | D. | $\sqrt{x+1}$=x-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com