
分析 (1)设方程的两个实数根为x1、x2,根据△≥0恒成立,x1•x2>0.x1+x2>0恒成立,即可证明.
(2)由方程的两个实数根为x1、x2,根据根与系数的关系即可解答
解答 解:(1)设方程的两个实数根为x1、x2,
△=(m2+3)2-4×$\frac{1}{2}$(m2+2)=m4+4m2+5=(m2+2)2+1≥0恒成立,
x1•x2=$\frac{1}{2}$(m2+2)>0恒成立,
x1+x2=m2+3>0恒成立,
∴无论m是任何实数,方程总有两个正根;
(2)∵x${\;}_{1}^{2}$+x${\;}_{2}^{2}$-x1x2=$\frac{17}{2}$,
∴(x1+x2)2-3x1x2=$\frac{17}{2}$,
∴(m2+3)2-3×$\frac{1}{2}$(m2+2)=$\frac{17}{2}$,
整理得:(2m2-1)(m2+5)=0
解得:m=±$\frac{\sqrt{2}}{2}$.
点评 本题考查了根与系数的关系及根的判别式,关键掌握x1,x2是方程x2+px+q=0的两根时,x1+x2=-p,x1x2=q.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
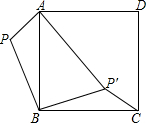 如图,已知P为正方形ABCD外的一点,PA=1,PB=2,将△ABP绕点B顺时针旋转90°,使点P旋转至点P′,且AP′=3,则∠BP′C的度数为 ( )
如图,已知P为正方形ABCD外的一点,PA=1,PB=2,将△ABP绕点B顺时针旋转90°,使点P旋转至点P′,且AP′=3,则∠BP′C的度数为 ( )| A. | 105° | B. | 112.5° | C. | 120° | D. | 135° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
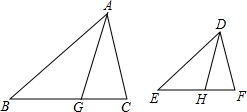 已知,如图,AG、DH分别是△ABC和△DEF的角平分线,且$\frac{AB}{DE}$=$\frac{BG}{EH}$=$\frac{AG}{DH}$,求证:△DEF∽△ABC.
已知,如图,AG、DH分别是△ABC和△DEF的角平分线,且$\frac{AB}{DE}$=$\frac{BG}{EH}$=$\frac{AG}{DH}$,求证:△DEF∽△ABC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 答对题数(道) | 12 | 13 | 14 | 15 |
| 人数 | 4 | 18 | 16 | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com